使用铣削约束进行拓扑优化_大众娱乐医疗器械注册站

使用铣削约束进行拓扑优化

新闻资讯 | 2024-09-09 13:46

SIMP 法:

优点：结构设计变量（单元密度）和优化问题直接挂钩对应，即拓扑结构explicitly dependent on设计变量。优化算法收敛好，灵敏度简单易算。可以直接进行基于有限元的离散设计灵敏度计算。适用于结合更复杂的非线性结构拓扑，比如几何非线性和材料非线性问题。

缺点：优化出来的拓扑结构边界不够清晰，特别是当过滤半径比较大的时候。这些灰度区域没有物理意义，设计如果无后处理无法直接用于制造。

Level-set 法：

优点：用一个高纬度的水平集implicitly表达拓扑结构的边界，从而解决了SIMP法的灰度区域问题。拓扑结果边界清晰，无灰度区域，设计可以直接用于制造。

缺点：由于设计变量间接与优化问题挂钩，中间涉及一些被水平集切割的有限单元的近似，从而影响优化精度。水平集方程需要用PDE方程来更新，中间还需要重置水平集方程来保证PDE的持续更新，从而大大降低优化收敛速度或者甚至无法收敛。PDE需要连续形状灵敏度来更新，相比SIMP的离散设计灵敏度更难。线弹性体的连续形状灵敏度已经发展很成熟，但是非线性结构连续形状灵敏度非常难求，需要很高的数学基础。

PS: 水平集是高维的，但是实现起来并不复杂。在原来有限元网格基础上再增加一个水平集网格就好了。

大连理工大学，西北工大，华中科技，清华。大工有程耿东院士，还有郭旭，他们做的MMV，MMC也算是有一定知名度了。提一点拓扑优化和增材制造可以算是天作之合了。

在变密度法的拓扑优化中有限元求解是其中的一个步骤，基本上可以把拓扑优化看做是在有限元分析之上的一层循环，循环内反复调用有限元求解器，每次有限元求解完毕后更新敏感度场，无量纲密度场，材料参数场等场变量，然后根据新的场变量再次调用有限元求解器，直到达到拓扑优化的收敛标准。

另一个关系是，有限元的单元刚度矩阵恰好就是（变密度法）拓扑优化的伴随矩阵，或者是伴随矩阵的组成部分。

地图学上有个叫图层的概念，就是点、线、面各专题要素分开。

如果不考虑撕开的话，可以把藏宝图用图层叠加的方式会更加有趣。

可以把各种位置参考的地理要素进行分开处理成多份要素地图。

如下做个示范：

1、从标准地图网站下载一幅标准地图用作藏宝图全图。

2、对图层中的信息要素进行分层处理。

3、把以上四份地图叠加。

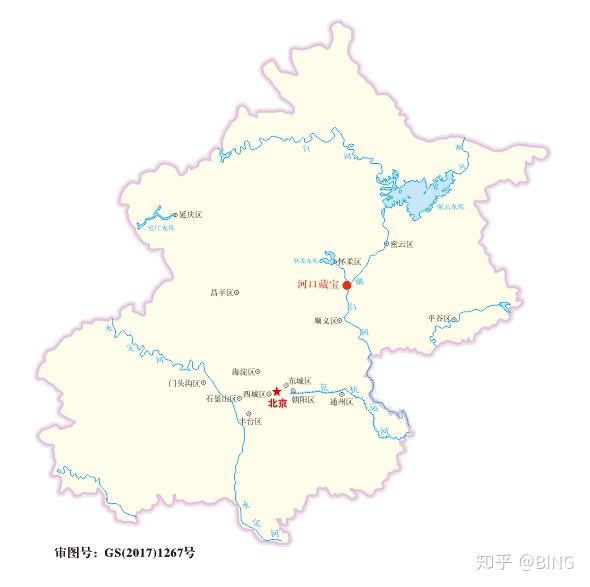
4、恭喜你，宝藏就在那，出发！

PS：当然如果更有趣、更详细的话，也可以添加路网交通、行政区划等相关信息，也可以增加附图的方式扩展详细信息内容。

确实和不变性有关，不过重点错了＞v＜不是量变和质变的关系，是（一定限制下的）形变而质不变。

这里的限制保持的是连续性，所以数学中的拓扑由开集族定义，并且研究与之相关、兼容（不破坏结构）的对象和问题。其他的例如网络这样的图结构，只要边连接相同就是相同的，这一点不变（或者作为特征、不变量）的前提下研究附加属性，所以也涉及拓扑这个概念。

至于“拓扑”这两个字，是音译，觉得不形象或者木得精髓，可以保留意见。用得多了，术语就是个代号，大家都懂就好。毕竟这个概念本身没有形象可言，翻成拓扑还是拖普不影响对于背后的理论和应用的认识。

其实对于这种原义不是很重要也不是很特别的专有名词，音译而非意译挺好的。毕竟语种之间词意的对应通常不构成映射。

讲个冷笑话：

对于functional group的理解，

数学上，functional是指泛函，group是指群（泛函群什么鬼）
化学上，functional group是正经表述，翻成中文是官能团（好有道理）

看了一些和我的研究方向比较相近的工作，这里做一下介绍吧，感觉还是挺有意思的。

对于凸函数，我们找极小点通常是考虑它的梯度流，即梯度下降算法。对于非凸的函数，梯度流的轨道是往局部极小点或者鞍点跑的。

如果不考虑函数本身的梯度，而是考虑某个程函方程 (等价于 H-J 方程) 的 (粘性) 解的梯度，就有可能找到全局极小点。这里其实把搜寻极小点的问题转化为了求解 PDE 的问题 (控制问题)。

在弱 KAM 理论中，当 Hamiltonian 对动量对称，相应的 Mane 临界值 $c(H)$ 就是 $H(x,0)$ 的全局最大值，此时考虑函数 $f(x)=-H(x,0)$ ，除了假设极小点集 $\\mathcal A$ 非空，基本上我们不需要什么额外的条件，就能通过对应的定态方程 $H(x,Du)=c(H)$ 的粘性解搜寻极小值点。此时梯度流是相对于粘性解而言的，而极小点集其实就是 Aubry 集。本质上，这个方法利用的是校准曲线的极限集总是落在 Aubry 集里面这个结论。

具体来说，考虑定态方程 $\\min f+\\frac{1}{2}|Du|^2=f(x).$ 令 $\\ell(x):=\\sqrt{2(f-\\min f)}$ ，那么 $u$ 也是程函方程 $|Du|=\\ell(x),\\ x\\in\\mathbb R^n\\backslash\\mathcal A$ 的解，满足边值条件 $u(x)=0,\\ x\\in\\mathcal A.$ 这个边值问题的解有表示 $u(x)=\\inf_{a}\\int_0^{t_x(a)}\\ell(y^a_x(s))ds,\\quad \\dot y^a_x(s)=a(s).$ 这里 $t_x(a)$ 为轨道 $y^a_x$ 第一次到达 $\\mathcal A$ 的时间， $a(s)$ 为控制函数， $y^a_x(0)=x$ 。可以证明极小的轨道几乎处处是沿着粘性解 $u(x)$ 的梯度跑的，并且在有限时间内 ( $dist(x,\\mathcal A)$ ) 达到全局极小点。

On the other hand, he (M. Powell) is probably partly responsible for the sceptical view that the classical optimization community always has held of random search methods, be they inspired by evolutionary analogues or not. He (M. Powell) believed that local optimality is all one can get in the nonconvex case.

We believe that global convergence is rather meaningless in practice. The pure random search converge with probability one to the global optimum of functions belonging to a broad class, where the main assumption is that a neighborhood of the global optimum should be reachable by the search distribution with a positive probability. However, the convergence rate is sub-linear with degree 1/n, therefore, the running time is proportional to $(1/\\epsilon)^n$ . Even for moderate dimension, e.g., n=10, this is prohibitively slow in practice.

“Fast convergence may be more important than global yet slow convergence, especially when considering the restart strategies.”

拓扑优化（Topology Optimization）是在给定的3D几何设计空间内对设计人员设置的定义规则集优化材料的布局及结构的过程。目标是通过对设计范围内的外力、荷载条件、边界条件、约束以及材料属性等因素进行数学建模和优化，从而最大限度的提高零件的性能。

传统的拓扑优化使用有限元分析来评估设计性能并生成满足以下目标的结构：

降低刚度重量比（Stiffness-to-Weight ratio）
具有更好的应变能重量比（strain energy to weight ratio）
降低材料体积及安全系数的比例（material volume to safety factor ratio）
自然频率重量比（natural frequency to weight ratio）

拓扑优化特别在工程产品设计中，被用于新产品的设计阶段，提高其刚度重量比。

由于拓扑优化生成的自由形式的设计通常难以用传统工业制造手段进行制造，但是在3D打印技术的进步条件下，拓扑优化的设计输出可以直接交给3D打印机来完成，极大的拓展了拓扑优化的工业化进程。

自21世纪初以来，拓扑优化概念已普遍应用于Solidworks、Autodesk等CAD软件应用程序中。

拓扑优化经常被误解并与衍生式设计混为一谈。这两种产品设计技术在过去十年中都很流行，但被人经常误解成同一种概念。

那么拓扑优化与衍生式设计有何区别？

拓扑优化需要用户提供设计模型，以及外力、约束条件以及材料属性等输入信息。然后通过FEA分析零件来去除多余的材料以生成优化的结果。因为拓扑优化需要一个工程产品设计者的初始模型（original model），由于初始模型的存在，其大大限制了工程师重新设计零件的可能性以及创新性。

从另一方面，拓扑优化是衍生式设计的一种技术手段。衍生式设计使用拓扑优化，并不依赖初始模型，使得设计过程更加的自由。衍生式设计通过获取设计空间、力或荷载、约束条件等输入信息来进行建模，然后使用形状优化来分析和创建多个设计供设计师选择和评估。Creo以及Autodesk等高级衍生式设计软件就可以自动生成大量设计稿并将其与预设的规则条件集进行比较。

这个过程将允许设计师快速迭代数百种甚至数千种可能的设计解决方案，以从海量的备选方案中选出最合适的优化方案。

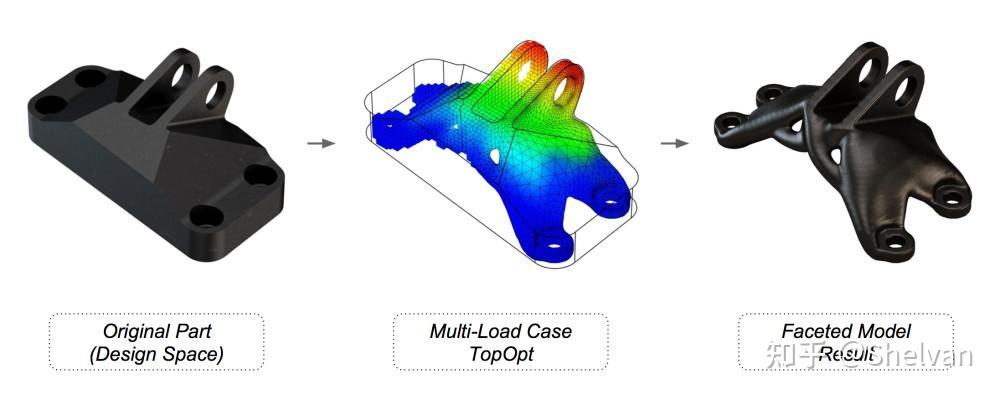
首先，设计人员确定零件所需的最小设计空间
定义外部荷载、边界条件、约束条件以及材料属性等输入信息（当然还指定了固定锚点）。
利用FEA考虑最小集合设计网络并将设计空间分解为更小的区域，例如应用负载点、安装位置以及约束区域。
拓扑优化使用有限元创建这个较小设计区域的基本网格（mesh），并通过FEA评估网格的应力分布和应变能，以找到每个元素可以处理的最佳载荷或者应力。
拓扑优化程序以数字方式从各个角度对设计施加应力，评价其结构完整性，并找到不需要的材料区域。
根据定义的要求测试每个有限元的刚度、柔度、应力、挠度，确定多余的材料区域。
最后，有限元分析将各个部件编织在一起组成设计终稿。

与任何其他设计工具或产品设计过程一样，拓扑优化有自己的优缺点。

优化设计——大多数时候，产品设计需要平衡各类因素并确定最佳的设计解决方案。FEA由于其可以提前考虑各类因素，所以可以极大程度上避免设计失败的可能性。
材料使用的最小化——拓扑优化最吸引的地方就是在于其可以减少不必要的重量。特别是在航空领域，每增加一克的配重就需要增加大量的设计成本。更轻的重量和更小的尺寸也就意味着更少的能耗。
具有成本效益——拓扑优化可以最大限度的减少材料的使用和成本。并且还节省了其他因素，例如包装、更少的移动和运输能源。拓扑优化产生的许多复杂的几何形状会使标准制造工艺变得“难以实现”，但是当3D打印的技术越发成熟，这种设计实现起来也不是那么困难。
减少对环境的影响——由于拓扑优化能够最大限度的减少材料的使用，所以其可以被定义为可持续设计。

成本提高——因为大多数拓扑优化设计只能适用于3D打印，所以跟一般传统制造方法相比，成本并不能减少。
强度降低——在某些情况下，减少材料的用量也就意味着结构整体强度无法跟优化之前的结果相提并论。

两者的区别还是很明显的；

目前各大CAD软件中的“拓扑优化”是引入材料性能以及受力位置等参数后，对一个型体进行分析，之后仅保留受力区域结构的一种算法

而CAD软件中的“创成式设计”指的是由计算机通过执行一系列的预先编好的算法后生成某种型体的过程。操作者不需要对型体的每个结构进行细致调整，在定义了一些参数特征后输入一系列特定程序后来让软件自己进行运算，最终得到一种型体。

“拓扑优化”，仅仅是“创成式设计”可以采用的算法的一种。

1 拓扑优化简介

材料的有效利用一直都是人类追求的目标，也是许多研究领域不变的话题，并伴随着结构优化理论和方法的产生而发展。结构优化设计通常分为三个层次:

（1）拓扑优化：在一个确定的连续区域内寻求结构内部非实体区域位置和数量的最佳配置，寻求结构中的构件布局及节点联结方式最优化，使结构能在满足应力、位移等约束条件下，将外载荷传递到结构支撑位置，同时使结构的某种性态指标达到最优；

（2）形状优化：指在保持结构拓扑不变的前提下，通过改变设计区域的边界和形状，寻找结构最佳的边界和几何形状，其优化变量通常为杆系结构的节点坐标，或者连续体结构的外形等；

（3）尺寸优化：指在保持结构拓扑和形状不变的前提下，寻找结构构件的最佳截面尺寸，优化变量通常为杆件的截面尺寸，或者板壳的厚度等。上述三个层次的优化设计，其设计难度由难到易，并且分别对应结构的概念设计阶段、基本设计阶段以及详细设计阶段。

与形状优化和尺寸优化相比，结构拓扑优化节省材料更为显著，基于结构拓扑优化的常见设计流程如下图所示：

目前常用与结构拓扑优化的手段很多，如基于matlab、hypermesh、ansys经典、ansys workbench等。由于ansys workbench 18.2在三维结构的拓扑优化设计方面具有一套完整的分析模块，如图2所示。包括了初始结构静力（模态）分析模块、拓扑优化分析模块、优化后结构的静力（模态）分析模块。

为了测试ansys workbench 18.2拓扑优化计算的正确性，根据文献[1]及文献[2]中提到的算例信息，在ansys workbench 18.2的拓扑优化模块中建立模型，并进行拓扑优化，讲计算结果与文献中的计算结果进行对比如下：

如图3所示，该结构为一平面简支梁，长 120mm，宽 20mm，厚 1mm，在梁跨中作用一集中荷载 F=1N。

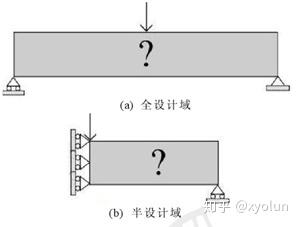
如图6所示，该结构为一平面悬臂梁，长 32mm，宽 20mm，厚 1mm,在梁右下角处受到一集中荷载作用，F=1N。

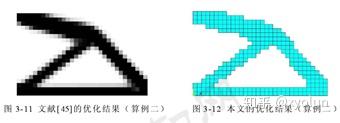
如图9所示，该结构为一平面悬臂梁，长 16mm，高 10mm，厚 1mm,在梁右端中部作用一集中荷载 F=300N。

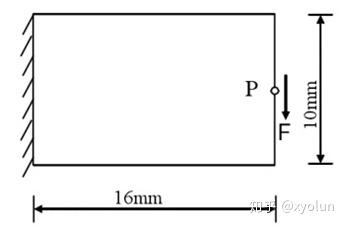
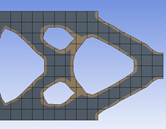
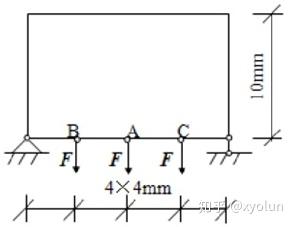
如图12所示，该结构为一平面简支梁，其基本尺寸为长 16mm，宽 10mm，厚 1mm。梁底部受到三个集中荷载的作用，F=1000N。

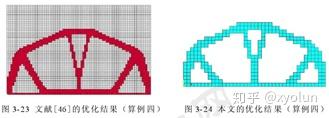
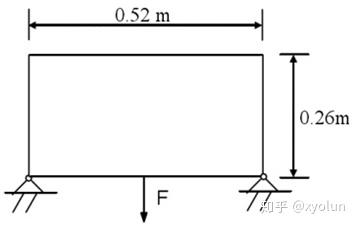
如图15所示，该结构为一平面超静定梁，长 520mm，宽 260mm，厚6mm，在梁下端中部受到一集中荷载作用，F=21000N。

如图18所示，天线面板是靠天线背架结构支撑的，背架结构主要由辐射梁组成，辐射梁的上弦节点通过一些支撑杆来和面板连接以达到支撑的效果。

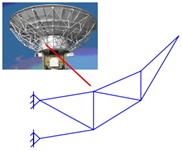
如图22所示，结构上部承受均布荷载，下方的两个支座为固定支座，进行拓扑优化分析，取剩余材料的10%，可以得到如图23所示的结果，可见，与常见的桥梁结构十分接近，可见该优化结构具有十分优秀的承载能力。

通过第二章的算例计算，可以看出Ansys workbench 18.2在拓扑优化领域具有较高的计算精度，能够将其应用在工程设计中。由于Ansys workbench 18.2拓扑优化中，初始结构中不能有惯性荷载，因此不能做受惯性荷载的结构优化。可能的应用方向为：（1）大跨度板壳类结构加筋肋的优化布置；（2）框架类结构基于最大（小）固有频率的槽钢优化布置。

对于大跨度板壳及受力较大的折弯板，目前均采用增加加强筋的方式增大结构强度、刚度。但是加强筋如何布置大部分来自于设计员的设计经验，这样就可能会导致设计过于保守或强度、刚度不足，可以通过优化设计计算加强筋材料的最优布置方式，然后综合考虑结构中其他部件的相互干涉问题，最终确定合理的加强筋布置方式。

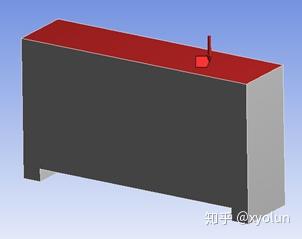
本节选用了一个100mm×100mm×100mm的油箱模型进行计算，考虑空油箱在内部均步压力作用及装满油的油箱在内部均步压力与静水压力共同作用下两种工况，计算相应的加强筋优化布置。

3.1.1均布压力作用下加强筋的优化布置

图25中，红色区域为油箱壁所在区域，蓝色部分为加强筋所在的区域，下面的计算只针对蓝色区域进行拓扑优化计算。

当设置剩余材料百分比为10%时，得到的优化结果如下：

当设置剩余材料百分比为20%时，得到的优化结果如下：

当设置剩余材料百分比为30%时，得到的优化结果如下：

当设置剩余材料百分比为35%时，得到的优化结果如下：

3.1.2均布压力+静水压力共同作用下加强筋的优化布置

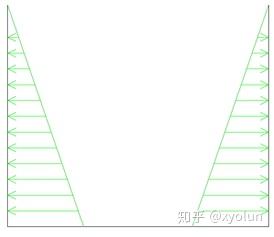
当设置剩余材料百分比为10%时，得到的优化结果如下：

当设置剩余材料百分比为20%时，得到的优化结果如下：

当设置剩余材料百分比为30%时，得到的优化结果如下：

当设置剩余材料百分比为35%时，得到的优化结果如下：

3.2.1四边简支板受板中心集中荷载作用

当设置剩余材料百分比为10%时，得到的优化结果如下：

设置剩余材料百分比为15%时，得到的优化结果如下：

百分比为20%时，得到的优化结果如下：

当设置剩余材料百分比为30%时，得到的优化结果如下：

3.2.1四边简支板受均布荷载作用

当设置剩余材料百分比为10%时，得到的优化结果如下：

设置剩余材料百分比为15%时，得到的优化结果如下：

当设置剩余材料百分比为20%时，得到的优化结果如下：

当设置剩余材料百分比为30%时，得到的优化结果如下：

对于承受动力荷载的结构，如风荷载、海浪荷载、地震荷载等。要求结构基频尽量避开激励力的频率，因此在结构设计时有时需要使结构频率尽可能大或者尽可能小。

如有下图所示一框架结构，红色部分两根槽钢可能需要用于开安装孔，因此纳入优化区域，中间蓝色部分为选定的拓扑优化区域，右端固定，左端无约束。通过计算得到使结构固有频率最大时的材料分布。

首先对原结构进行模态分析，计算得到结构优化前后，前六阶固有频率及前三阶振型图如下所示：

原结构前六阶频率：444HZ,801HZ,1900HZ,2084HZ,2405HZ,2792HZ

优化后结构前六阶频率：685HZ,701HZ,1099HZ,1255HZ,1817HZ,1865HZ

相应的振型图如下图所示：

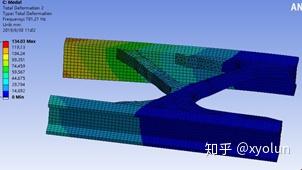
可以看出，通过拓扑优化，寻找到如图所示的结构布置，能够使结构的基频显著提高，而且去除了80%的材料，既节省了材料，减轻了结构自重，又达到了提高结构基频的目的。

[1]板壳结构加劲肋拓扑优化方法研究_马强

[2]基于变密度法的连续体结构拓扑优化研究_吴顶峰

今天我们再来谈谈adjoint method。

比方说我们要在方程约束之下优化函数：

$\\begin{align}&\\min ~F(x) \\\\ &\ ext{subject to}~~ A(z)x=b \\end{align}$

其中 $x$ 是场量， $b$ 是source，他们之间的关系由物理规律 $A(z)x=b$ 给出，其中 $z$ 是涉及的参数（一般是待设计的器件的参数）。下面我们要求FoM函数 $F$ 对参数 $z$ 的梯度。这里为了方便，我们讨论 $F$ 不直接依赖于 $z$ 的情况。如果有依赖，只要加一项偏导即可。

我线性代数学的不太好，所以推导会写成求和的形式。如果你喜欢写成更简洁的矩阵形式也是完全没问题的。

我们先讨论实数情况。根据chain rule：

$\\frac{dF}{dz_{i}}=\\sum_{j}\\frac{\\partial F}{\\partial x_{j}}\\frac{\\partial x_{j}}{\\partial z_{i}}$

先算 $\\frac{\\partial x_{j}}{\\partial z_{i}}$ ：

$[A(z) + \\frac{\\partial A}{\\partial z_{i}}dz_{i}](x+dx)=b$

$A(z)dx=-(\\frac{\\partial A}{\\partial z_{i}}dz_{i})x$

写成单个分量：

$\\frac{\\partial x_{j}}{\\partial z_{i}}=-[A^{-1}(\\frac{\\partial A}{\\partial z_{i}})x]_{j}$

下面求 $\\frac{dF}{dz_{i}}$ ：

$\\begin{align}\\frac{dF}{dz_{i}}&=\\sum_{j}\\frac{\\partial F}{\\partial x_{j}}[-A^{-1}\\frac{\\partial A}{\\partial z_{i}}x]_{j}\\\\ &=-\\sum_{j}\\sum_{k}\\frac{\\partial F}{\\partial x_{j}}(A^{-1})_{jk}(\\frac{\\partial A}{\\partial z_{i}}x)_{k}\\\\ &=-\\sum_{j}\\sum_{k}(\\frac{\\partial A}{\\partial z_{i}}x)_{k}(A^{T})^{-1}_{kj}\\frac{\\partial F}{\\partial x_{j}}\\\\ &=-\\sum_{k}(\\frac{\\partial A}{\\partial z_{i}}x)_{k}[(A^{T})^{-1}\\frac{\\partial F}{\\partial x}]_{k}\\end{align}$

我们把 $-(A^{T})^{-1}\\frac{\\partial F}{\\partial x}$ 记做 $x^{\ ext{adj}}$ ，也就是所谓的adjoint field。它满足方程

$A^{T}x^{\ ext{adj}}=-\\frac{\\partial F}{\\partial x}$

所以为了求得adjoint，我们只需要先算出每个点处FoM对场的梯度 $\\frac{\\partial F}{\\partial x}$ ，然后再解一个线性方程组就可以了。这个操作称为adjoint simulation，计算复杂度接近于一次forward simulation。事实上如果你对optimal control有了解，或者熟悉神经网络的反向传播，那么这些内容都是非常简单直接的。

这样，我们最终要求的梯度就可以写成：

$\\frac{dF}{dz_{i}}=(\\frac{\\partial A}{\\partial z_{i}}x)^{T}x^{\ ext{adj}}$

在电磁学中，矩阵 $A$ 对 $z$ 的偏导数往往形式比较简单。比如说要解TM模的电场， $A$ 具有形式：

$A=D^{H}_{x}\\mu_{yy}^{-1}D^{E}_{x}+ D^{H}_{y}\\mu_{xx}^{-1}D^{E}_{y}+ \\epsilon_{zz}$

设计变量是介电常数，那么 $A$ 只有第i个对角元依赖于 $z_{i}$ ，计算得到极大简化。对于TE模会麻烦一点，但你会发现如果令 $z=\\epsilon^{-1}$ ， $\\frac{\\partial A}{\\partial z_{i}}$ 跟 $z_{i}$ 无关，是可以提前计算出来的。

用adjoint辅助计算的好处在于高效。你当然可以换种方式，比如说直接计算 $A^{-1}\\frac{\\partial A}{\\partial z_{i}}x$ 。这时候，对于每个 $z_{i}$ ，你在计算出 $\\frac{\\partial A}{\\partial z_{i}}x$ 之后，都需要解一个线性方程组。这显然是非常耗时的，毕竟参数的数目往往挺大的。当然也不是不可以直接计算 $A^{-1}\\frac{\\partial A}{\\partial z_{i}}x$ ，比如Shanhui组最近的paper[1]。

如果场量是复数（对电磁学模拟来说很正常），唯一的变化在于chain rule里面不仅要有对 $x$ 的偏导数，还要有对 $x^{*}$ 的偏导数：

$\\begin{align}\\frac{dF}{dz_{i}}&=\\sum_{j}\\frac{\\partial F}{\\partial x_{j}}\\frac{\\partial x_{j}}{\\partial z_{i}}+ \\frac{\\partial F}{\\partial x^{*}_{j}}\\frac{\\partial x^{*}_{j}}{\\partial z_{i}}\\\\ &=2\ ext{Re}(\\sum_{j}\\frac{\\partial F}{\\partial x_{j}}\\frac{\\partial x_{j}}{\\partial z_{i}}) \\end{align}$

后面的计算过程都是一样的。

对于FDFD，用上述框架理解完全没有问题。如果是FDTD，就需要一点数学知识：forward simulation是ODE/PDE在时间上的前向演化，adjoint simulation则是adjoint equation在时间上的后向演化。具体可以参考我之前写的那篇adjoint method。

只要求得梯度，那么设计器件也就变成一个简单的梯度下降问题啦！当然实际上没有那么简单，因为我们会希望设计出来的器件方便fabrication（很重要！）。具体来说，折射率应当是接近binary的，而且对加工过程中的error要足够鲁棒。这些问题有很多方式可以处理，我之后会简单介绍。

最后我要针对[2]做一点说明（出自Yablonovitch组）。论文截图：

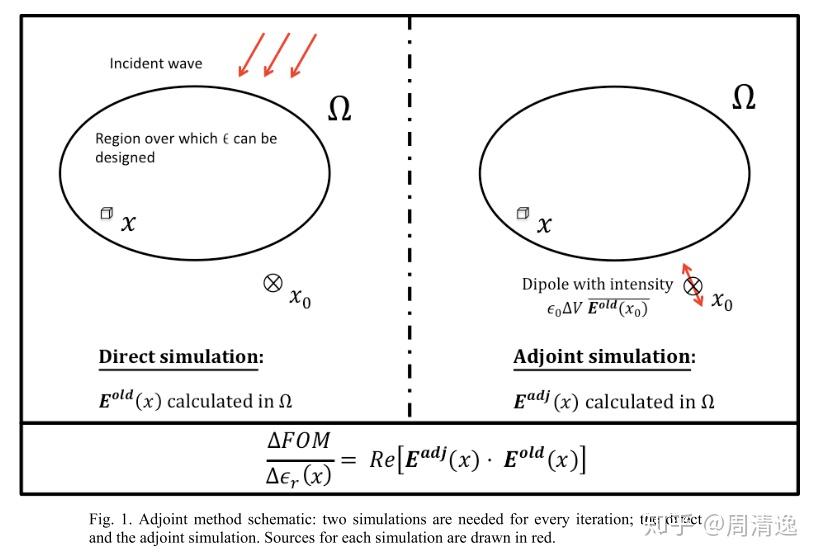
这个图看上去很清晰直观：一次forward simulation，然后在FoM对场的梯度不为0的点（图里是一个点 $x_{0}$ ）放置一个dipole source，进行adjoint simulation，从而得到FoM对各个点 $x$ 处介电常数的梯度。

但是他们在推导的过程中用到很多表示差分的记号，比如 $\\Delta V$ 、 $\\Delta \\epsilon_{r}$ 。明明用正常的微积分语言几行就能写清楚，论文中却一直用 $\\Delta$ ，不仅在严谨性上打了折扣，还容易造成误解。

[1]Forward-Mode Differentiation of Maxwell's Equations

[2]Adjoint shape optimization applied to electromagnetic design

发电厂在冬季可以利用热电联产达到高效供电。它是如何做到的呢？依靠区域热网。以前，这种网络设计仅限于小型网络的线性模型或非线性模型。最近的研究表明，我们可以使用基于梯度的优化的非线性模型设计大型网络（参考文献 2）。本文我们将使用 COMSOL Multiphysics? 软件及其附加的管道流和优化模块重现这项研究。

供应电力的发电厂通常将不到一半的输入能量转换成电能。通过捕获发电过程中产生的热量可以提高效率，这些热量可以为城市的住宅供暖。

为了实现这种供暖系统，必须构建一个用于分配热量的管道网络。这项技术在冬天可以使发电厂的效率高达80％（参考资料1）！

来自德国 Tübingen 的区域热管示例。图片来源：Bj?rnAppel。通过Wikimedia Commons在CC BY-SA 3.0下获得许可。

本篇博文中讨论的模型考虑了相同的用户、连续的管道直径以及散热器和网络热损失的简单模型。这意味着最终生成的拓扑网络可能会很好，但是为了让定量的管道直径更有可信度，使用更高级的表达式和技术可能很有必要，如参考文献 2 中所描述的那样。

优化问题包括控制、约束和目标三个因素。下面，我们来看一看这些因素对于优化问题有关的意义。

区域热网通常与道路基础设施保持一致，因此可以将网络设计方式的问题简化为以下问题：

哪条道路应该有管道？
这些管道应该多大？

消费者通常要为过热的热水付费，因为这浪费了泵送能量。因此，消费者希望能够降低通过换热器的流速，该换热器用于将热网连接到住宅物业的加热系统。但是，这可能会导致系统中的流速过低；从而使得热网到地面存在热量散失，进而导致距发电厂较远的消费者家里的温度较低。为避免这个问题，热网的末端配备了旁通阀，以确保末端用户有足够的流量。

因为我们不知道网络的终点，所以只是简单的将每个生产者都视为旁通阀，并优化了该阀的直径。我们还针对个人用户优化了散热器控制，从而有效地确定了用户级别的室温与网络加热流体之间的耦合常数。最后，我们可以优化网络上的驱动压力。

为了使网络有效，它必须能够分配足够的热量给所有消费者，大型网络会拥有更多的消费者，从而导致了许多约束，造成计算量巨大。解决这个问题的一种惯用方法是使用约束聚合技术，将大量的线性约束转换为单一的非线性约束，即

$C=\\frac{\\log(\\sum_{i=1}^{N_\\mathrm{consumers}}\\exp(\\beta\\left(P/P_\\mathrm{target}-1\\right)^2))}{\\beta N_\\mathrm{consumers}}< 1\\\\$

对局部约束的违反将随着 $\\beta$ 值的增大而减少，但是较大的值也会引起数值问题。因此，在实践中，必须找到一种折衷的办法。

建立网络的主要成本与挖掘沟渠的总长度有关，且较大的管道比较小的管道成本更高，因此我们可以将估算成本：

$\\mathrm{EUR}_\\mathrm{pipes}=\\int_\\mathrm{roads}(a D + b ) dl\\\\$

这里，D 是管道直径，b 是挖沟渠的成本，a 是一个参数，这表明了一个事实：购买和安装更大的管道成本更高。值 a 和 b 是根据参考文献 1估算的。

就其本身而言，这将导致一个具有非常小的管道和较大压降的网络，从而需要昂贵的泵。我们可以通过添加与泵送功率相关的项来避免这种情况，因此总目标函数变为

$\\mathrm{EUR}_\\mathrm{total}=\\mathrm{EUR}_\\mathrm{pipes}+ P_\\mathrm{pump}1000[EUR/W]\\\\$

将泵送功率与目标函数相关联的常数取决于几个因素，例如网络的维护成本、电价和资本成本。

每个用户需要 5kW 的热能。消费者以与城市街区相对应的矩形排列，而矩形又依次排列成阵列。消费者被排列在对应于城市街区的矩形中，这些矩形依次以阵列的形式重复。该网络有一个制热器，为西南角输送 70°C 的水，另一个制热器在北部输送 65°C 的水。

该模型从优化旁路和散热器控制开始，将约束 C 作为目标函数。当最小化 $\\mathrm{EUR}_\\mathrm{total}$ 时，这一结果被用作计算的初始值。

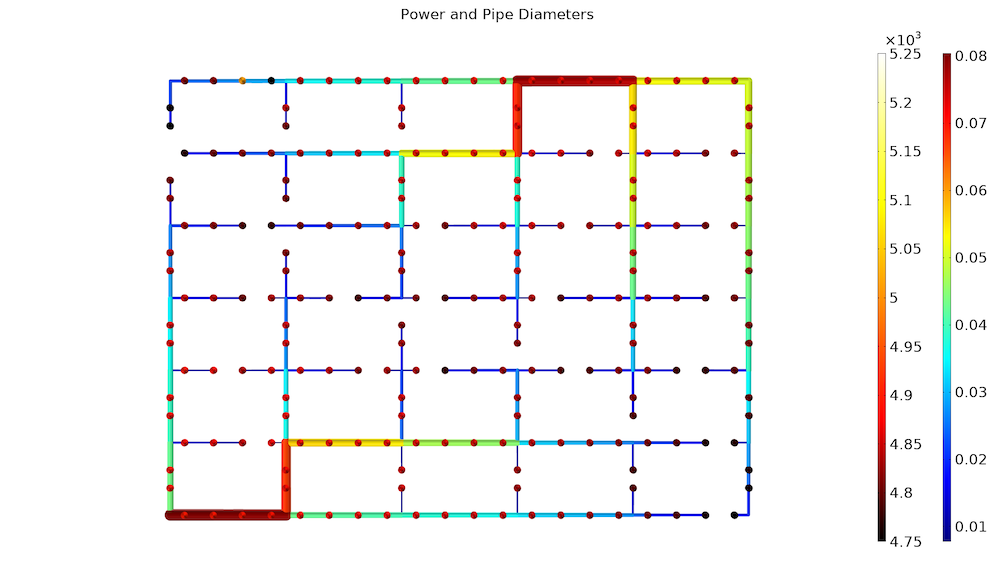
第一张图显示了优化后的每个用户的管道直径以及加热功率。网络设计分支变成越来越小的管道，这是在意料之中的。在这里案例下，我们考虑这样一种情况，即几乎到处都有消费者的情况，因此很难减少 $\\mathrm{EUR}_\\mathrm{Pipe}$ 。

显示了网络拓扑以及用户的加热功率。最小功率为 4.7kW，因此没有一个用户会感觉寒冷。

第二个图显示了旁路控制的值。正如预期的那样，除了两个网络的最末端，阀门大部分都是关闭的。

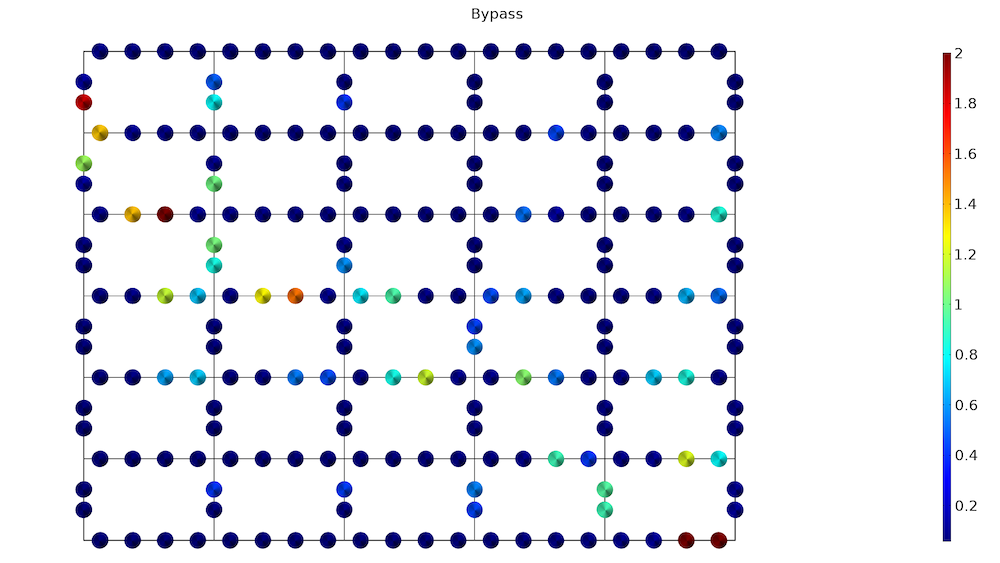
最后，我们可以查看用户散热器控制，并得出结论：热网中入口温度为 65°C 的用户相比处于更高温度热网的用户需要将他们的散热器调高一点。在进行优化计算时，散热器控制的最大限制参数设一个较大的值，从而计算过程中不会达到该上限值，降低该上限值意味着允许用户使用性能一般的散热器，但在网络末端使用更好的散热器，整体经济成本可能会更低。人们可以通过在目标函数中包含散热器的成本来优化这个问题。

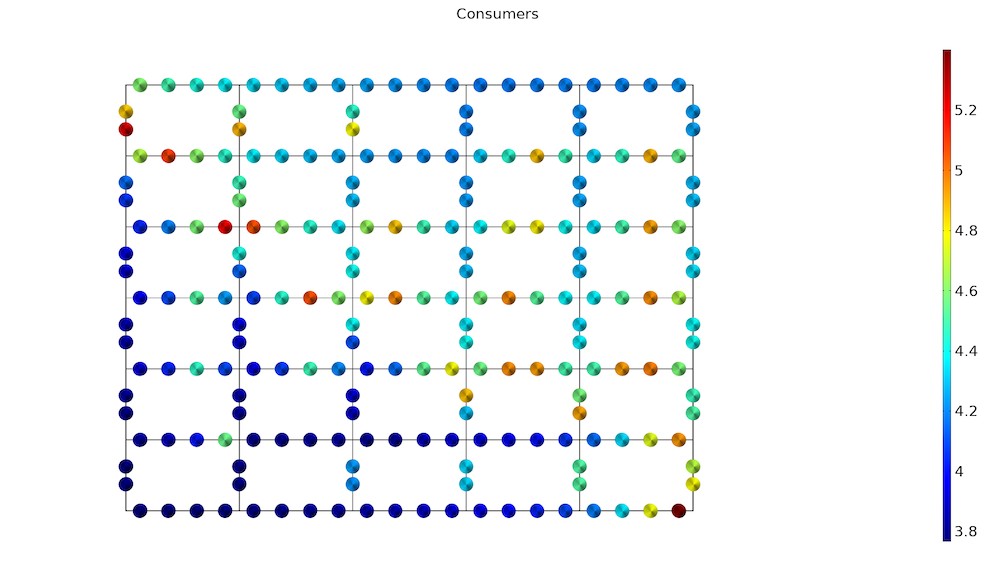
您可以使用参考文献 2 中使用的技术扩展模型。编写一个模型方法支持从 OpenStreetMap;导入道路网络，并创建用于设计分布式供热网络的仿真 App。该仿真 App 可以告诉我们需要购买哪些管道，并为消费者估算成本，以评估建立网络的可行性。

创建用于设计分布式供热网络的仿真 App 区域供热网络的拓扑优化

“How Gas Turbine Power Plants Work”, Office of Fossil Energy, https://www.energy.gov/fe/how-gas-turbine-power-plants-work.
M. Blommaert, Y. Wack, and M. Baelmans, “An adjoint optimization approach for the topological design of large-scale district heating networks based on nonlinear models”, Applied Energy, vol. 280, 2020.

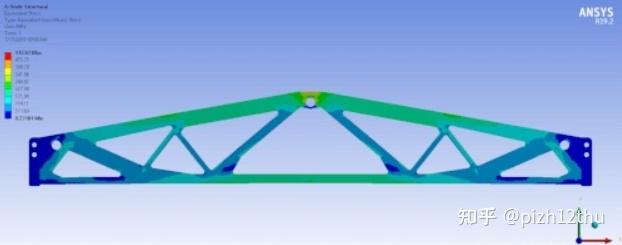
上一篇解决了2D三角形的像素化，接下来考虑3D空间中三角形网格的体素化。体素(Voxel)可以理解为二维像素在三维空间的推广，它们是一组分布在正交网格中心的立方体单元。体素网格在仿真分析中通常用在拓扑优化的计算中，即栅格法，这样生成的网格是正六面体，非常方便高精度计算，每个优化步骤删除若干体素网格，并不会破坏模型的整体拓扑特性，网格利用率比较高。通过体素网格的变化去逼近实体材料结构的分布，比如ANSYS中的经典桥梁模型。常见的三角网格模型体素化算法分为表面体素化和内部体素化这2个步骤。

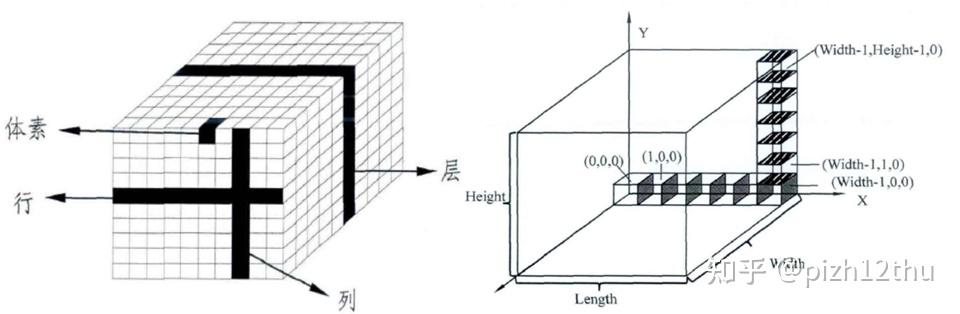
表面体素化算法分为5类:

第一类是直接求取三角形与体素距离的算法，计算可能与三角形相交的所有体素到三角形平面的距离，通常需要考虑大量不与三角形相交的体素, 计算效率较低。

第二类是将三角形投影到二维，求取2D平面上与三角形相交的格子，再将格子恢复至三维求取三维体素。但投影平面上相交的格子恢复至3D空间时对应的相交体素并不唯一，因此会丢失部分与三角形相交的体素。

第三类是选取三角形的某些点，以点体素化代替三角形体素化，运算速度较快，但同样会丢失部分与三角形相交的体素。

第四类是采用硬件加速的算法，将三维体素空间划分为若干个二维切面，利用GPU 进行二维切面的体素化，再合并成三维，需要硬件支持，且通常不能得到准确的相交体素。

第五类仍是投影到二维的算法，不直接计算与三角形相交的二维格子，而是计算这些格子的顶点，将这些格子顶点恢复至三维，再寻找三维体素，这能够找全与三角形相交的体素，但每个相交体素可能被找到多次，运算效率会受到影响。

内部体素化算法中，种子填充算法效率较高, 被广泛应用，包括扩散法和基于扫描射线的种子填充算法。此外还包括类似种子填充算法的Flooding 算法，基于四面体的内部体素化算法，以及基于深度缓存原理的内部体素化算法等。

对于种子填充算法，基于扫描射线的算法相比传统的扩散法对于单个体素具有更小的计算量，后面将使用扫描射线法进行。

这里采用投影到二维的算法，记三角网格模型的物理坐标的最小值和最大值分别为xmin, xmax, ymin, ymax, zmin, zmax, 以(xmin, ymin,zmin)和(xmax, ymax, zmax)为对角顶点建立一个各边均平行于坐标轴的立方体，即该网格模型的AABB包围盒。将包围盒的与x 轴平行、与y 轴平行和与z轴平行的边分别进行等分，分段数量分别为NX,NY,NZ，3 个方向上每一段的长度分别为dx, dy, dz. 过等分点用垂直于被等分边的平面将包围盒内部进行分割，将包围盒分割为NX×NY×NZ 个立方体，这些立方体即为体素。

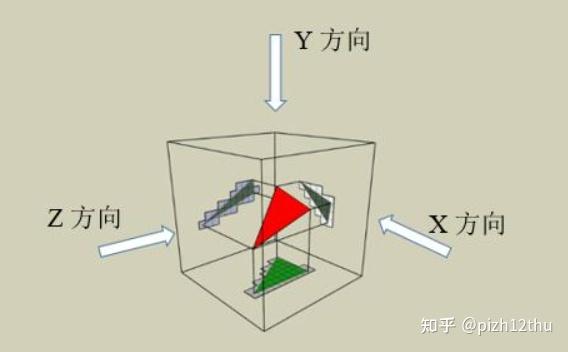
将三角形分别正交投影到3个坐标轴平面，相当于从包围盒的边界用三个方向的光线射线去照射三角形，得到在二维投影平面内三角形内部的像素点（光照阴影），然后反求内部像素点的深度坐标Z，从而得到与三角形相交的体素位置。

下面通过代码和公式讲解。首先定义一些存储结构，之前在读取STL文件时采用了（N,3,3）数组保存三角网格数据，这里继续使用。

meshXYZ - Nx3x3 array - 3维数组定义N个三角面片的顶点位置信息： 
                                  DIM1 N个三角面
                                  DIM2 每个顶点的3个坐标
                                  DIM3 每个三角面的3个顶点

gridX   - integer - X方向分段数NX.
gridY   - integer - Y方向分段数NY.
gridZ   - integer - Z方向分段数NZ.
raydirection - String    - 定义射线扫描的方向，默认'xyz',做三次投影扫描，合并最终结果

gridOUTPUT - PxQxR logical array - 三维体素数组，网格内部标记为1，外部为0
gridCOx    - (P,) array - X 方向分段坐标点.
gridCOy    - (Q,) array - Y 方向分段坐标点.
gridCOz    - (R,) array - Z 方向分段坐标点.

以Z方向的投影和射线为例，首先得到网格中坐标极值，确定扫描范围，在投影平面上确定XY坐标像素点范围

    # Identify the min and max x,y,z coordinates (cm) of the mesh:
    meshXmin = meshXYZ[:,0,:].min()
    meshXmax = meshXYZ[:,0,:].max()
    meshYmin = meshXYZ[:,1,:].min()
    meshYmax = meshXYZ[:,1,:].max()
    meshZmin = meshXYZ[:,2,:].min()
    meshZmax = meshXYZ[:,2,:].max()

    # Identify the min and max x,y coordinates (pixels) of the mesh:
    meshXminp = np.where( np.abs(gridCOx-meshXmin)==np.abs(gridCOx-meshXmin).min() )[0][0]
    meshXmaxp = np.where( np.abs(gridCOx-meshXmax)==np.abs(gridCOx-meshXmax).min() )[0][0]
    meshYminp = np.where( np.abs(gridCOy-meshYmin)==np.abs(gridCOy-meshYmin).min() )[0][0]
    meshYmaxp = np.where( np.abs(gridCOy-meshYmax)==np.abs(gridCOy-meshYmax).min() )[0][0]

    # Make sure min < max for the mesh coordinates:
    if meshXminp > meshXmaxp:
        meshXminp,meshXmaxp = meshXmaxp,meshXminp
    if meshYminp > meshYmaxp:
        meshYminp,meshYmaxp = meshYmaxp,meshYminp

    # Identify the min and max x,y,z coordinates of each facet:
    meshXYZmin = np.min(meshXYZ,axis=2)
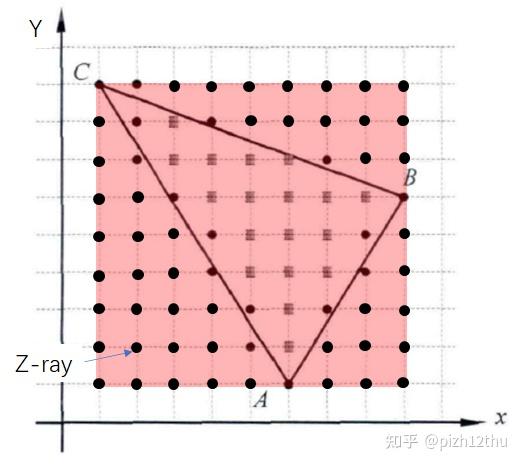
    meshXYZmax = np.max(meshXYZ,axis=2)

接下来循环XY平面上的像素点，判断Z方向射线穿过哪些三角形(投影)。首先找到射线的平面坐标（x，y）均落在三角形的包围盒内的像素点，满足 $x_{min}\\leq x \\leq x_{max}$ 且 $y_{min}\\leq y \\leq y_{max}$ ，得到射线可能穿过的三角形的ID——possibleCROSSLIST，在possibleCROSSLIST中进一步采样判断。

    correctionLIST = np.zeros((0,2),dtype=int) # N x 2
    # Loop through each x,y pixel.
    # The mesh will be voxelised by passing rays in the z-direction through
    # each x,y pixel, and finding the locations where the rays cross the mesh.
    for loopY in range(meshYminp,meshYmaxp+1):
        # - 1a - Find which mesh facets could possibly be crossed by the ray:
        possibleCROSSLISTy = np.where( (meshXYZmin[:,1]<=gridCOy[loopY]) & (meshXYZmax[:,1]>=gridCOy[loopY]) )[0]

        for loopX in range(meshXminp,meshXmaxp+1):       
            # - 1b - Find which mesh facets could possibly be crossed by the ray:
            possibleCROSSLIST = possibleCROSSLISTy[ (meshXYZmin[possibleCROSSLISTy,0]<=gridCOx[loopX]) & (meshXYZmax[possibleCROSSLISTy,0]>=gridCOx[loopX]) ]
            # continue operation follow
            ......
            ......

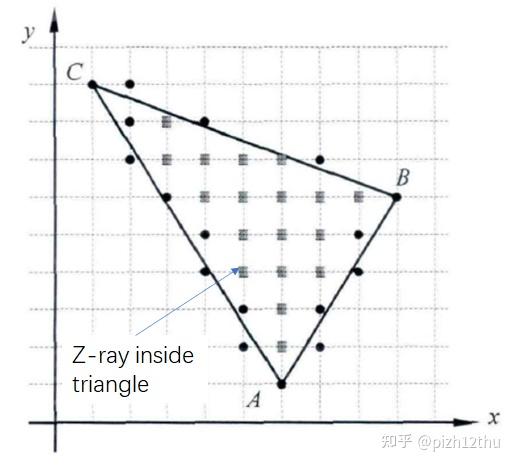
接下来判断哪些射线真正"穿过"了三角形，即哪些像素点在三角形内部或边界。在上篇中已经实现了一种基于向量叉积的判断算法，

pizh12thu：STL模型像素化/体素化过程实现(1)

这里可以直接应用，找到内部像素点。这里形式上做了一些规整，其中

$\\begin{cases}Y1_{predicted}=y_1-(y_1-y_2)*(x_1-x_0)/(x_1-x_2)\\\\ YR_{predicted}=y_1-(y_1-y_2)*(x_1-x)/(x_1-x_2)\\\\ \\end{cases}\ ag{1}$

$\\begin{cases}Y1_{predicted}-y_0>0\\\\ YR_{predicted}-y>0\\end{cases}\\Rightarrow \\begin{cases}(y_1-y_0)(x_1-x_2)-(y_1-y_2)*(x_1-x_0)>0\\\\ (y_1-y)(x_1-x_2)-(y_1-y_2)*(x_1-x)>0\\\\\\end{cases}\ ag{2}$

式（2）即为叉积表达式 $\\bar{P_1P_0}\ imes\\bar{P_1P_2}$ 和 $\\bar{P_1Q}\ imes\\bar{P_1P_2}$ ，计算结果同号则表示 $P_0$ 、 $Q$ 两点均在 $\\bar{P_1P_2}$ 边的同侧（同左或同右），依次判断三条边，都同号则 $Q$ 点在三角形内。把在三角形内部和边界的像素坐标保存到facetCROSSLIST中。

     if possibleCROSSLIST.size > 0:  
         # 判断给出的坐标是否在闭合的三角形中，向量叉积法
         for loopCHECKFACET in possibleCROSSLIST.flatten():
         #Check if ray crosses the facet.  This method is much (>>10 times) faster than using the built-in function 'inpolygon'.
         #Taking each edge of the facet in turn, check if the ray is on the same side as the opposing vertex.
         Y1predicted = meshXYZ[loopCHECKFACET,1,1] - ((meshXYZ[loopCHECKFACET,1,1]-meshXYZ[loopCHECKFACET,1,2]) * (meshXYZ[loopCHECKFACET,0,1]-meshXYZ[loopCHECKFACET,0,0])/(meshXYZ[loopCHECKFACET,0,1]-meshXYZ[loopCHECKFACET,0,2]))
         YRpredicted = meshXYZ[loopCHECKFACET,1,1] - ((meshXYZ[loopCHECKFACET,1,1]-meshXYZ[loopCHECKFACET,1,2]) * (meshXYZ[loopCHECKFACET,0,1]-gridCOx[loopX])/(meshXYZ[loopCHECKFACET,0,1]-meshXYZ[loopCHECKFACET,0,2]))
                        
         if (Y1predicted > meshXYZ[loopCHECKFACET,1,0] and YRpredicted > gridCOy[loopY]) or (Y1predicted < meshXYZ[loopCHECKFACET,1,0] and YRpredicted < gridCOy[loopY]):
                #The ray is on the same side of the 2-3 edge as the 1st vertex.
                Y2predicted = meshXYZ[loopCHECKFACET,1,2] - ((meshXYZ[loopCHECKFACET,1,2]-meshXYZ[loopCHECKFACET,1,0]) * (meshXYZ[loopCHECKFACET,0,2]-meshXYZ[loopCHECKFACET,0,1])/(meshXYZ[loopCHECKFACET,0,2]-meshXYZ[loopCHECKFACET,0,0]))
                YRpredicted = meshXYZ[loopCHECKFACET,1,2] - ((meshXYZ[loopCHECKFACET,1,2]-meshXYZ[loopCHECKFACET,1,0]) * (meshXYZ[loopCHECKFACET,0,2]-gridCOx[loopX])/(meshXYZ[loopCHECKFACET,0,2]-meshXYZ[loopCHECKFACET,0,0]))
                        
                if (Y2predicted > meshXYZ[loopCHECKFACET,1,1] and YRpredicted > gridCOy[loopY]) or (Y2predicted < meshXYZ[loopCHECKFACET,1,1] and YRpredicted < gridCOy[loopY]):
                   #The ray is on the same side of the 3-1 edge as the 2nd vertex.
                   Y3predicted = meshXYZ[loopCHECKFACET,1,0] - ((meshXYZ[loopCHECKFACET,1,0]-meshXYZ[loopCHECKFACET,1,1]) * (meshXYZ[loopCHECKFACET,0,0]-meshXYZ[loopCHECKFACET,0,2])/(meshXYZ[loopCHECKFACET,0,0]-meshXYZ[loopCHECKFACET,0,1]))
                   YRpredicted = meshXYZ[loopCHECKFACET,1,0] - ((meshXYZ[loopCHECKFACET,1,0]-meshXYZ[loopCHECKFACET,1,1]) * (meshXYZ[loopCHECKFACET,0,0]-gridCOx[loopX])/(meshXYZ[loopCHECKFACET,0,0]-meshXYZ[loopCHECKFACET,0,1]))
                                
                   if (Y3predicted > meshXYZ[loopCHECKFACET,1,2] and YRpredicted > gridCOy[loopY]) or (Y3predicted < meshXYZ[loopCHECKFACET,1,2] and YRpredicted < gridCOy[loopY]):
                       #The ray is on the same side of the 1-2 edge as the 3rd vertex.
                       #The ray passes through the facet since it is on the correct side of all 3 edges
                       facetCROSSLIST = np.insert(facetCROSSLIST,facetCROSSLIST.size,loopCHECKFACET,0)

得到了投影平面上的像素坐标，下面需要计算射线Z方向上的坐标，即在哪些“深度”穿过了三角面片。遍历facetCROSSLIST，确定三角形所在的平面 $Ax + By + Cz + D=0$ ，平面参数的求解式子如下：

$A=y_0 (z_1 - z_2) + y_1 (z_2 - z_0) + y_2 (z_0 - z_1)\\\\\ ag{3-1}$ $B=z_0 (x_1 - x_2) + z_1 (x_2 - x_0) + z_2 (x_0 - x_1)\\\\\ ag{3-2}$ $C=x_0 (y_1 - y_2) + x_1 (y_2 - y_0) + x_2 (y_0 - y_1)\\\\\ ag{3-3}$ $D=- x_0 (y_1 z_2 - y_2 z_1) - x_1 (y_2 z_0 - y_0 z_2) - x_2 (y_0 z_1 - y_1 z_0)\\\\\ ag{3-4}$

                    #----------
                    # - 3 - Find the z coordinate of the locations where the ray crosses each facet or vertex:
                    #----------
                    gridCOzCROSS = np.zeros(facetCROSSLIST.shape)
                    for loopFINDZ in facetCROSSLIST:
                        planecoA = meshXYZ[loopFINDZ,1,0]*(meshXYZ[loopFINDZ,2,1]-meshXYZ[loopFINDZ,2,2]) + meshXYZ[loopFINDZ,1,1]*(meshXYZ[loopFINDZ,2,2]-meshXYZ[loopFINDZ,2,0]) + meshXYZ[loopFINDZ,1,2]*(meshXYZ[loopFINDZ,2,0]-meshXYZ[loopFINDZ,2,1])
                        planecoB = meshXYZ[loopFINDZ,2,0]*(meshXYZ[loopFINDZ,0,1]-meshXYZ[loopFINDZ,0,2]) + meshXYZ[loopFINDZ,2,1]*(meshXYZ[loopFINDZ,0,2]-meshXYZ[loopFINDZ,0,0]) + meshXYZ[loopFINDZ,2,2]*(meshXYZ[loopFINDZ,0,0]-meshXYZ[loopFINDZ,0,1]) 
                        planecoC = meshXYZ[loopFINDZ,0,0]*(meshXYZ[loopFINDZ,1,1]-meshXYZ[loopFINDZ,1,2]) + meshXYZ[loopFINDZ,0,1]*(meshXYZ[loopFINDZ,1,2]-meshXYZ[loopFINDZ,1,0]) + meshXYZ[loopFINDZ,0,2]*(meshXYZ[loopFINDZ,1,0]-meshXYZ[loopFINDZ,1,1])
                        planecoD = - meshXYZ[loopFINDZ,0,0]*(meshXYZ[loopFINDZ,1,1]*meshXYZ[loopFINDZ,2,2]-meshXYZ[loopFINDZ,1,2]*meshXYZ[loopFINDZ,2,1]) - meshXYZ[loopFINDZ,0,1]*(meshXYZ[loopFINDZ,1,2]*meshXYZ[loopFINDZ,2,0]-meshXYZ[loopFINDZ,1,0]*meshXYZ[loopFINDZ,2,2]) - meshXYZ[loopFINDZ,0,2]*(meshXYZ[loopFINDZ,1,0]*meshXYZ[loopFINDZ,2,1]-meshXYZ[loopFINDZ,1,1]*meshXYZ[loopFINDZ,2,0])
                        
                        if abs(planecoC) < 1e-14: 
                            planecoC=0
                        else:
                            gridCOzCROSS[facetCROSSLIST==loopFINDZ] = (- planecoD - planecoA*gridCOx[loopX] - planecoB*gridCOy[loopY]) / planecoC

                    #Remove values of gridCOzCROSS which are outside of the mesh limits (including a 1e-12 margin for error).
                    gridCOzCROSS = gridCOzCROSS[ (gridCOzCROSS>=meshZmin-1e-12) & (gridCOzCROSS<=meshZmax+1e-12) ]
                    #Round gridCOzCROSS to remove any rounding errors, and take only the unique values:
                    gridCOzCROSS = np.round(gridCOzCROSS*1e12)/1e12
                    gridCOzCROSS = np.unique(gridCOzCROSS)

得到的深度坐标去重并保存在 gridCOzCROSS 中。

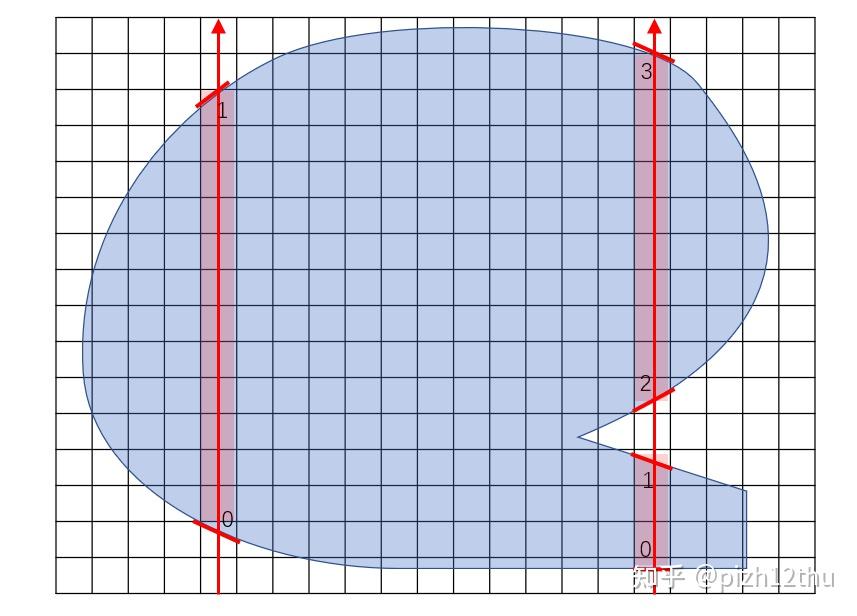
下一步，基于射线扫描的检测结果，应用扫描线种子填充算法计算内部体素。如果一个射线穿过封闭模型，那么必然有偶数个三角面与射线相交，并且对偶三角形之间的体素都在模型内部，如(0,1),(2,3)...(2k-2, 2k-1)。

                    #----------
                    # - 4 - Label as being inside the mesh all the voxels that the ray passes through after crossing one facet before crossing another facet:
                    #----------
                    # Only rays which cross an even number of facets are voxelised
                    if gridCOzCROSS.size % 2 == 0:  
                        for loopASSIGN in np.arange( 1, (gridCOzCROSS.size/2)+1,dtype=int ):
                            voxelsINSIDE = ((gridCOz>gridCOzCROSS[2*loopASSIGN-2]) & (gridCOz<gridCOzCROSS[2*loopASSIGN-1]))
                            gridOUTPUT[loopX,loopY,voxelsINSIDE] = 1

                    elif gridCOzCROSS.size > 0:
                        # Remaining rays which meet the mesh in some way are not voxelised, but are labelled for correction later.
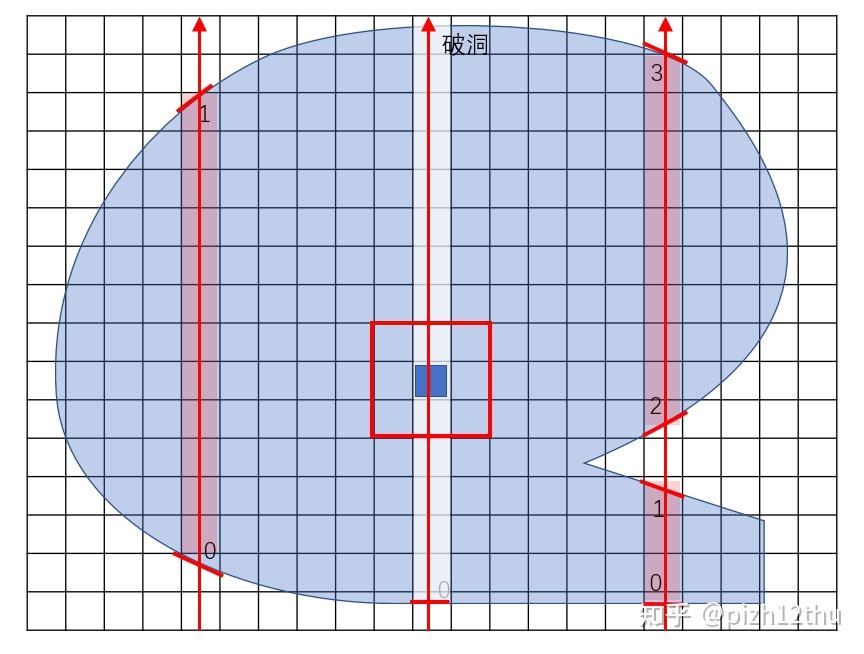
                        correctionLIST = np.insert( correctionLIST, correctionLIST.shape[0], [[loopX,loopY]], axis=0 )

如果模型完全不封闭，或者有游离的面片在网格内部，那么有些射线可能穿过奇数个三角面，使用插值法填充无法体素化的射线。为了保证边缘的插值可以进行，需要扩充体素数组的边界，以0填充。在目标体素点XY平面周围的8个像素点中计算，如果一半以上的体素被标记为内部，则目标体素也会被标记为内部，如图所示，如果射线超出模型表面，则周围体素被标记数量小于4。

    #======================================================
    # USE INTERPOLATION TO FILL IN THE RAYS WHICH COULD NOT BE VOXELISED
    #======================================================
    #For rays where the voxelisation did not give a clear result, the ray is computed by interpolating from the surrounding rays.
    countCORRECTIONLIST = correctionLIST.shape[0]

    if countCORRECTIONLIST>0:
        #If necessary, add a one-pixel border around the x and y edges of thearray.  
        #This prevents an error if the code tries to interpolate a ray at the edge of the x,y grid.
        if correctionLIST[:,0].min()==1 or correctionLIST[:,0].max()== gridCOx.size or correctionLIST[:,1].min()==1 or correctionLIST[:,1].max()==gridCOy.size:
            gridOUTPUT     = np.pad(gridOUTPUT,((1,1),(1,1),(0,0)),mode='constant')
            correctionLIST = correctionLIST + 1
        
        for loopC in np.arange( 0,countCORRECTIONLIST):
            voxelsforcorrection = np.sum( np.array([gridOUTPUT[correctionLIST[loopC,0]-1,correctionLIST[loopC,1]-1,:] ,\\
                                        gridOUTPUT[correctionLIST[loopC,0]-1,correctionLIST[loopC,1],:]   ,\\
                                        gridOUTPUT[correctionLIST[loopC,0]-1,correctionLIST[loopC,1]+1,:] ,\\
                                        gridOUTPUT[correctionLIST[loopC,0],correctionLIST[loopC,1]-1,:]   ,\\
                                        gridOUTPUT[correctionLIST[loopC,0],correctionLIST[loopC,1]+1,:]   ,\\
                                        gridOUTPUT[correctionLIST[loopC,0]+1,correctionLIST[loopC,1]-1,:] ,\\
                                        gridOUTPUT[correctionLIST[loopC,0]+1,correctionLIST[loopC,1],:]   ,\\
                                        gridOUTPUT[correctionLIST[loopC,0]+1,correctionLIST[loopC,1]+1,:] ,\\
                                        ]),axis=0 ) 
            voxelsforcorrection = (voxelsforcorrection>=4)
            gridOUTPUT[correctionLIST[loopC,0],correctionLIST[loopC,1],voxelsforcorrection] = 1
        #Remove the one-pixel border surrounding the array, if this was added
        #previously.
        if gridOUTPUT.shape[0]>gridCOx.size or gridOUTPUT.shape[1]>gridCOy.size:
            gridOUTPUT = gridOUTPUT[1:-1,1:-1,:]
 
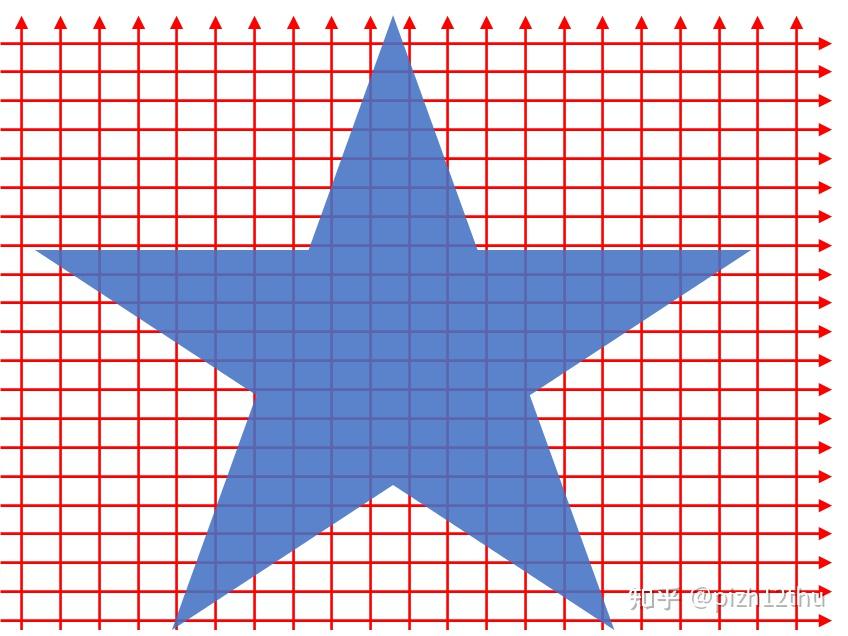
    return gridOUTPUT

在三个平面方向上投影保证每个三角形（包括垂直于坐标轴方向的）都能被检测到，避免了某些垂直边缘被舍弃，但是同一个位置的体素可能被标记多次，因此必须设定阈值来进一步合并和过滤。上面Z轴投影的程序可以复用，封装成 _VOXELISE 函数，调换传入体素数组各轴的顺序即可实现不同方向的投影体素化。

    # Prepare logical array to hold the voxelised data:
    gridOUTPUT      = np.zeros( (voxcountX,voxcountY,voxcountZ,len(raydirection)), dtype=bool)
    countdirections = 0
    
    if raydirection.find('x') + 1:
        gridOUTPUT[:,:,:,countdirections] = np.transpose(_VOXELISE(gridCOy,gridCOz,gridCOx,meshXYZ[:,[1,2,0],:]),(2,0,1))
        countdirections = countdirections + 1
    if raydirection.find('y') + 1:
        gridOUTPUT[:,:,:,countdirections] = np.transpose(_VOXELISE(gridCOz,gridCOx,gridCOy,meshXYZ[:,[2,0,1],:]),(1,2,0))
        countdirections = countdirections + 1
    if raydirection.find('z') + 1:
        gridOUTPUT[:,:,:,countdirections] = _VOXELISE(gridCOx,gridCOy,gridCOz,meshXYZ)
        countdirections = countdirections + 1

    # Combine the results of each ray-tracing direction:
    if len(raydirection)>1:
        gridOUTPUT = np.sum(gridOUTPUT,axis=3)>=len(raydirection)/2

体素显示

体素显示可以利用matplotlib中的gca.voxels()函数简单绘制，当然这个功能目前比较简陋，视图不能旋转拉伸等操作，只能看看正交视图，不过对于目前的测试也够用了。

from mpl_toolkits.mplot3d import Axes3D  # 这一句虽然显示灰色，但是去掉会报错。
import matplotlib.pyplot as plt

def showVoxel(voxel):
    fig = plt.figure()
    ax = fig.gca(projection='3d')
    ax.voxels(voxel,edgecolors='k',linewidth=0.5)
    ax.set(xlabel='X', ylabel='Y', zlabel='Z')
    ax.set_xlim([0,max(voxel.shape)])
    ax.set_ylim([0,max(voxel.shape)])
    ax.set_zlim([0,max(voxel.shape)])
    plt.show()

if __name__=='__main__':

    model1 = 'shoemodel.stl'
    model2 = 'photograph.stl'

    NX= int(56)
    NY= int(28)
    NZ= int(35)

    start=time.time()
    [gridOUTPUT,gridCOx,gridCOy,gridCOz] = voxelise.VOXELISE(NX,NY,NZ,model2,raydirection='xyz')
    print('gridOUTPUT\
',gridOUTPUT.sum())
    print('Python time:{:6f}'.format(time.time()-start))
    showVoxel(gridOUTPUT)

找个STL模型来测试一下，显示效果如下，对含有多个封闭模型的网格能够很好地划分体元。

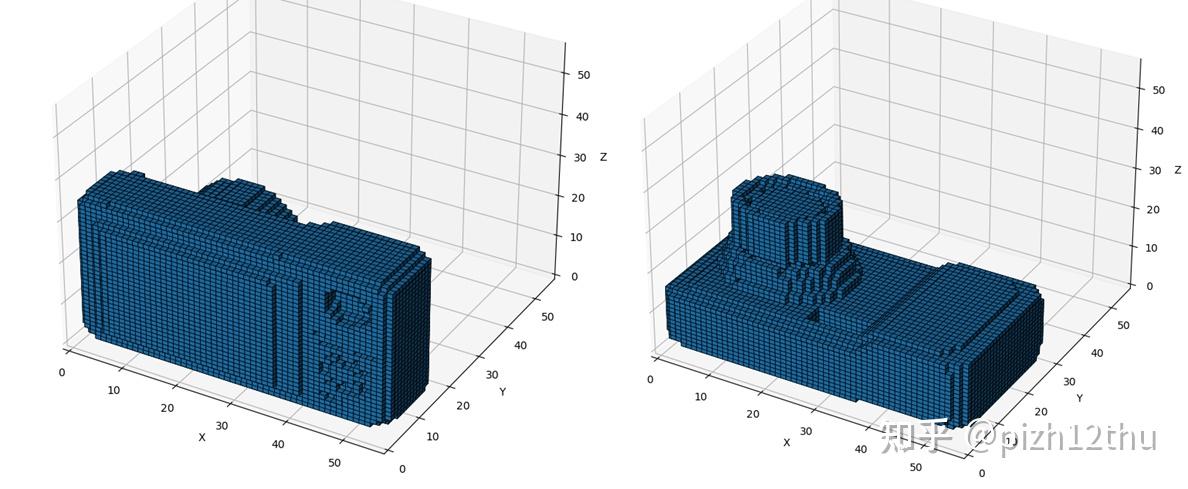
在体素化实现过程中，采用三角形平面求交方式确定“深度”，涉及大量的浮点数乘除运算，并且采用了双重循环扫描方式，并且需要遍历网格中所有三角形，循环方式在python中效率很低。考虑转换成成C++代码并在外层循环使用openMP并行加速，通过pybind11编译成python模块使用，对于多网格模型效率增加20倍以上。

import time
import numpy as np
import voxelise
import cvoxelise


from mpl_toolkits.mplot3d import Axes3D  # 这一句虽然显示灰色，但是去掉会报错。
import matplotlib.pyplot as plt

def showVoxel(voxel):
    fig=plt.figure()
    ax=fig.gca(projection='3d')
    ax.voxels(voxel,edgecolors='k',linewidth=0.5)
    ax.set(xlabel='X', ylabel='Y', zlabel='Z')
    ax.set_xlim([0,max(voxel.shape)])
    ax.set_ylim([0,max(voxel.shape)])
    ax.set_zlim([0,max(voxel.shape)])
    plt.show()


if __name__=='__main__':

    model1='shoemodel.stl'
    # model2='photograph.stl'
    NX=int(80)
    NY=int(200)
    NZ=int(20)
    # NX=int(56)
    # NY=int(28)
    # NZ=int(35)

    start=time.time()
[gridOUTPUT,gridCOx,gridCOy,gridCOz]=voxelise.VOXELISE(NX,NY,NZ,model1,raydirection='xyz')
    print('gridOUTPUT\
',gridOUTPUT.sum())
    print('Python time:{:6f}'.format(time.time()-start))


    vox=cvoxelise.Voxel()
    vox.initSize(NX,NY,NZ)
    start=time.time()
    gridOUTPUT=vox.VOXELISE(model1,parallel=True)
    print('gridOUTPUT\
',gridOUTPUT.sum())
    print('C Parallel:{:6f}'.format(time.time()-start))
    # showVoxel(gridOUTPUT)

生成 100000 左右体素的结果对比：

gridOUTPUT
131429
Python time: 4.042053
gridOUTPUT
131429
C Parallel: 0.175998

3D模型体素化（Voxelization）过程实现与分析（一）_新安浅滩的博客-CSDN博客_体素化

吴晓军, et al. (2005). "基于八叉树的三维网格模型体素化方法." 工程图学学报(04): 1-7.

吴耕宇, et al. (2015). "利用几何求交实现三角网格模型快速体素化." 计算机辅助设计与图形学学报 27(11): 2133-2141

经过前期若干节有限元的学习，终于到达了图穷匕见的时刻，便于总结，直接把之前的匕首们摆上了：

派大西：基元巧合：用有限元方法求解一维Poisson方程派大西：基元巧合（下篇）：用有限元方法求解二维Poisson方程派大西：基元巧合（前传）:有限元求解二维悬臂梁位移派大西：基元巧合（四）：矩形区域上的双线性元

经过这么多有限元的磨练，其最终目的其实是解锁结构拓扑优化技能。那么什么是拓扑优化？

大概是这么个事情，记得有个造桥的游戏，在给定材料的同时需要保证足够的结实，换到前几节的悬臂梁语境中，在相同的材料下，考虑下图中三种构建方式，显然，第一种快撑不住了，第二种的形变较小，第三种形变更小，貌似更加符合我们的需求。

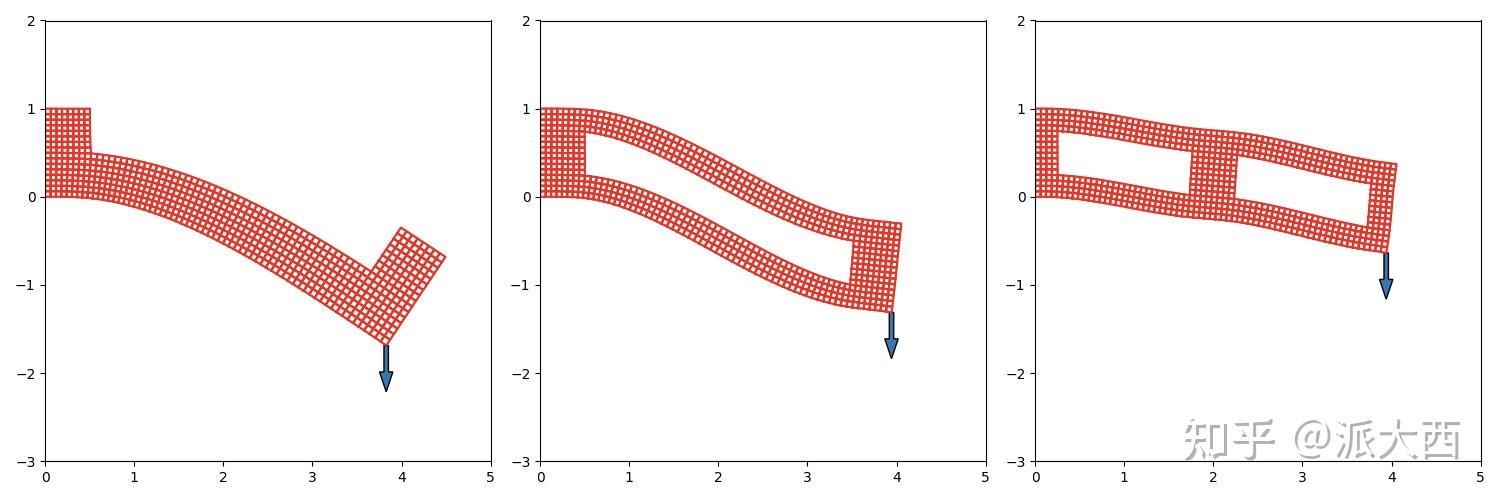
那么这就是最好的设计了吗？应该不是，这只是派大西的随手一画，要优化，还先得建模。

本文参考的是这篇古老文章：

Sigmund, Ole. "A 99 line topology optimization code written in Matlab." Structural and multidisciplinary optimization 21.2 (2001): 120-127.

不过这篇文章数学符号着实有些令（我这个外行）人费解，所以接下来会包含很多脑补内容。首先直接写出模型吧：

$\\begin{align}\\min_{x}\\quad &\\frac{1}{2}u^TK(x)u\\\\ s.t. \\quad &K(x)u=F\\\\ &x\\in[0,1]^N\\\\ &V(x)=V_0 \\end{align}\\\\$

来一行行看

第一行，是系统总势能，类比中学的弹性势能公式 $\\frac{1}{2}kx^2$ . u是整个系统中节点位移，由约束等式也可以变换为极小化 $u^TF$ ， $x$ 是设计变量，维数跟有限元单元数保持一致， $x_i=0$ 时表示第i个位置是空的， $x_i=1$ 表示该位置是实的，也就是放置材料。
第二行，约束条件，前几节已经求解了很多次了，K是刚度矩阵，线性依赖于x；F是载荷矩阵，由甲方需求决定，认为是不变的常数。
第三行，x是0/1二值变量，不提了。
第四行，整体材料的总用量，理解为 $\\sum x_i=V_0$ 就行

然后就是修整这个非凸二值优化问题，首先是松弛 $x$ 这种二值向量为连续向量，也就是

$0\\leq x\\leq 1 \\\\$

但如果x的某些分量为0的话，K会变成奇异矩阵，那么在数值上设置一个很小的正数作为下限，也就是

$0 < x_m\\leq x\\leq 1 \\\\$

另一方面，为了使数值变得偏向两端（0与1），用 $x^p$ （p>1）替代 $x$ ，那么原始的优化问题变成了

$\\begin{align}\\min_{x}\\quad &u^TF\\\\ s.t. \\quad &K(x^p)u=F\\\\ &0 < x_m\\leq x_e\\leq 1\\\\ &\\sum x_e=V_0 \\end{align}\\\\$

也等同于优化

$\\begin{align}\\min_{x}\\quad &\\sum x_e^p u_e^TK_0u_e\\\\ s.t. \\quad &K(x^p)u=F\\\\ &0 < x_m\\leq x_e\\leq 1\\\\ &\\sum x_e=V_0 \\end{align}\\\\$

基于梯度法迭代求解，需要知道目标函数对各个分量的偏导数，

$\\begin{align}c(x)=u^TF\\\\ \\end{align}\\\\$

其中 $u$ 满足 $K(x^p)u=F$ ，那么 $u$ 是个关于 $x$ 的函数。对一个有显示表达式的函数求偏导数是挺简单的，但这种带有约束的形式倒是稍微少见点，求解 $c(x)$ 对某个 $x_e$ 分量的话，需要用到所谓的伴随法：

$\ ilde c(x,\ ilde u)=u^TF+\ ilde u^T(K(x^p)u-F) \\\\$

那么

$\\begin{align}\\frac{\\partial \ ilde c}{\\partial x_e}=F^T\\frac{\\partial u}{\\partial x_e}+px_e^p\ ilde u^TK_eu+\ ilde u^TK(x^p)\\frac{\\partial u}{\\partial x_e}\\end{align}\\\\$

那么乘子 $\ ilde u$ 应满足

$F^T=-\ ilde u^TK(x^p) \\\\$

也就说明 $\ ilde u=-u$ ，代入其中，得到

$\\frac{\\partial c}{\\partial x_e}=\\frac{\\partial \ ilde c}{\\partial x_e}=-px_e^{p-1}\ ilde u^TK_eu \\\\$

伴随法还有不少用途，来日方称。当然，能穿透参数化的优化问题求导本身也是个挺有趣的事情：

Agrawal, Akshay, et al. "Differentiable convex optimization layers." arXiv preprint arXiv:1910.12430 (2019).

利用这些记号，原问题变成了

$\\begin{align}\\min_{x}\\quad &c(x)\\\\ s.t. \\quad &0 < x_m\\leq x_e\\leq 1\\\\ &\\sum x_e=V_0 \\end{align}\\\\$

是个线性约束下的可微的优化问题了，此时求解有不少选择，下面继续使用原教旨的做法对该问题的进行求解。

接下来就用迭代法对以上问题进行启发式更新，通常所谓的“启发”，就是“看起来有些道理做起来效果也还行但理论上如何work我也不太了解的意思”。那么观察一下这个问题：

$\\begin{align}\\min_{x}\\quad &c(x)\\\\ s.t\\quad &\\sum x_e=V_0 \\end{align}\\\\$

改写成极小极大的形式：

$\\begin{align}\\min_{x}\\max_{\\lambda}\\quad &c(x)+\\lambda(\\sum x_e-V_0)\\\\ \\end{align}\\\\$

那么更新准则就分为两部分，一部分是更新乘子 $\\lambda$ ，使上式变大。另一部分是更新设计变量 $x$ ，使上式变小。

更新 $\\lambda$ ，采用二分法更新，不断缩小 $[\\lambda_l, \\lambda_u]$ 区间的范围。也就是说:

当 $\\sum x_e\\geq V_0$ 时，将区间更新为 $[\\lambda_m, \\lambda_u]$
当 $\\sum x_e < V_0$ 时，将区间更新为 $[\\lambda_l, \\lambda_m]$

其中 $\\lambda_m$ 是区间的中点

更新 $x$ ，对极小极大问题求导：得到

$\\frac{\\partial L}{\\partial x_e}=\\frac{\\partial c}{\\partial x_e}+\\lambda \\\\$

如果上式大于0，则说明应该减小 $x_e$ ；
如果上式小于0，则说明应该增大 $x_e$ ；
如果上式为0，则x保持不变

那么定义

$B_e=\\frac{-\\frac{\\partial c}{\\partial x_e}}{\\lambda}\\\\$

如果上式大于0，则 $B_e < 1$ ，则说明应该减小 $x_e$ ；
如果上式小于0，则 $B_e > 1$ ，则说明应该增大 $x_e$ ；
如果上式为0，则 $B_e=1$ ，则 $x_e$ 保持不变

由这三点，就可以推出更新准则为

$x_e :=x_eB_e^\\eta,\\quad(\\eta > 0,) \\\\$

考虑 $x_e$ 的上下限约束，以及不要步子迈得太大，做一些限制，最后配合上两个到区间的投影算子，得到更新准则为：

$x_e=\\mathbf{Proj}_{[x_m,1]}\\left(\\mathbf{Proj}_{[x-m,x+m]}(x_eB_e^\\eta)\\right) \\\\$

代码是这样：

def OC(nelx: int, nely: int, x: np.ndarray, volfrac: float, dc: np.ndarray):
    l1, l2, move = 0., 1e5, 0.2
    xnew = np.zeros_like(x)
    while l2 - l1 > 1e-4:
        lmid = (l1 + l2) / 2
        xnew = np.maximum(0.001, np.maximum(x - move, np.minimum(1., np.minimum(x + move, x * np.sqrt(-dc / lmid)))))
        if xnew.sum() - volfrac * nelx * nely > 0:
            l1 = lmid
        else:
            l2 = lmid
    return xnew

这一步其实也是挺启发式的，大意是 $x_e$ 或者 $\\frac{\\partial c}{\\partial x_e}$ 关于 $e$ 的空间分布变化过于剧烈，最后优化出来的东西难以制造（想象国际象棋棋盘那种黑白变化的微结构），需要对解或者导数进行光滑化处理，对于某个形状单元e进行光滑化，需要在附近的形状单元上定义出权重：

$H_f=\\max(0,1-dist(e,f)) \\\\$

另一个需要考虑的权重是 $x_e$ 本身的大小，综合起来，光滑化后的对 $x_e$ 偏导数为：

$\\overline{\\frac{\\partial c}{\\partial x_e}}=\\frac{\\sum_fH_fx_f\\frac{\\partial c}{\\partial x_e}}{\\sum_f H_fx_f}\\\\$

不同的光滑化算子会得到不同结构，还可以考虑

$\\overline{\\frac{\\partial c}{\\partial x_e}}=\\frac{\\sum_fH_f\\frac{\\partial c}{\\partial x_e}}{\\sum_f H_f}\\\\$

或者原文中的

$\\overline{\\frac{\\partial c}{\\partial x_e}}=\\frac{\\sum_fH_fx_f\\frac{\\partial c}{\\partial x_e}}{x_e\\sum_f H_f}\\\\$

光滑化的效果如下：

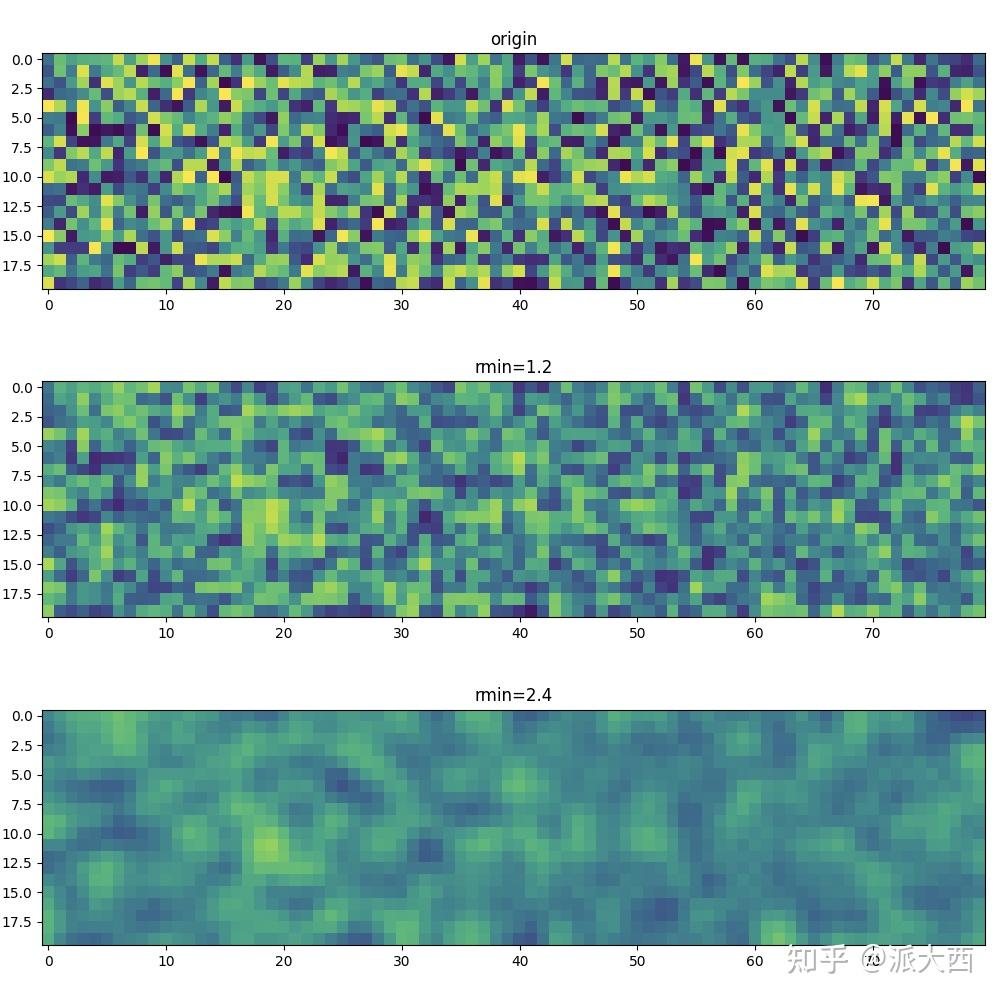
当然，直接用scipy自带的高斯滤波器之类的滤一下应该也问题不大，会比下面这段不太python风格的代码高效得多：

def smooth(nelx: int, nely: int, rmin: float, x: np.ndarray, dc: np.ndarray):
    dcn=np.zeros_like(dc)
    for i in range(nelx):
        for j in range(nely):
            sum_=0.
            for k in range(max(i - round(rmin), 0), min(i + round(rmin) + 1, nelx)):
                for l in range(max(j - round(rmin), 0), min(j + round(rmin) + 1, nely)):
                    fac=rmin - np.sqrt((i - k) ** 2 + (j - l) ** 2)
                    sum_ +=max(0, fac) * x[l, k]
                    dcn[j, i]+=max(0, fac) * x[l, k]* dc[l, k]
            dcn[j, i]=dcn[j, i]/ sum_
    return dcn

然后还是引言中的问题，设置 $V_0$ 为512，用原文中的光滑化算子的话，得到

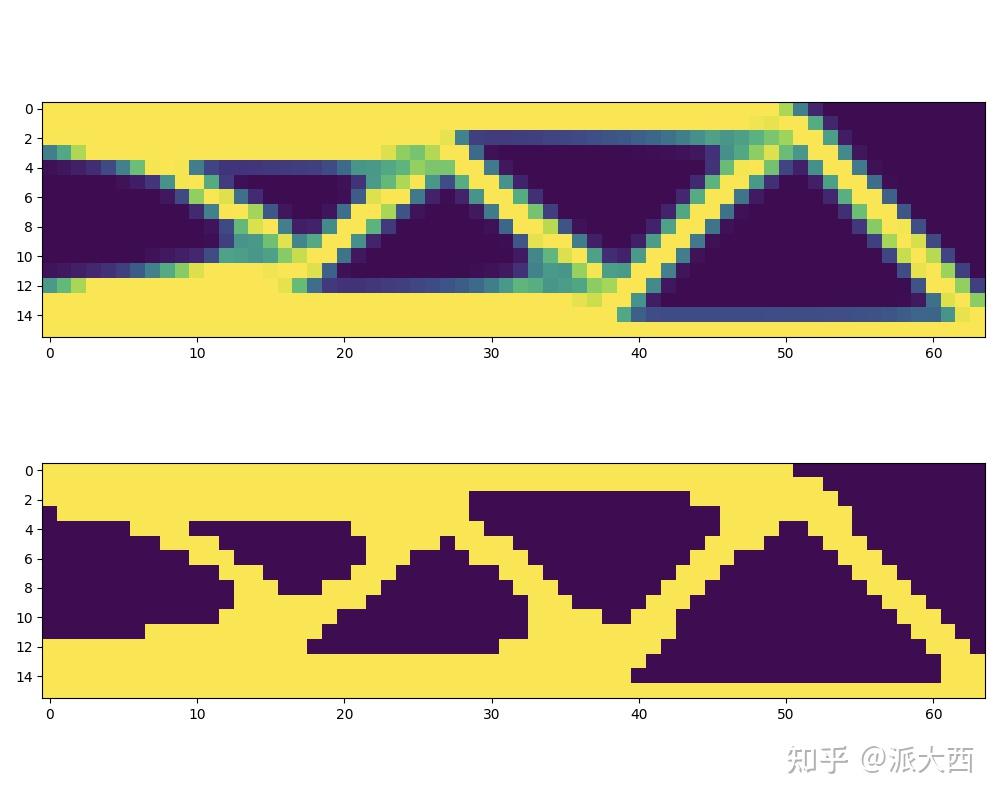
换成第二个光滑算子，可以得到这样，这个貌似还需要更精细的网格，但结构还是非常对称漂亮的：

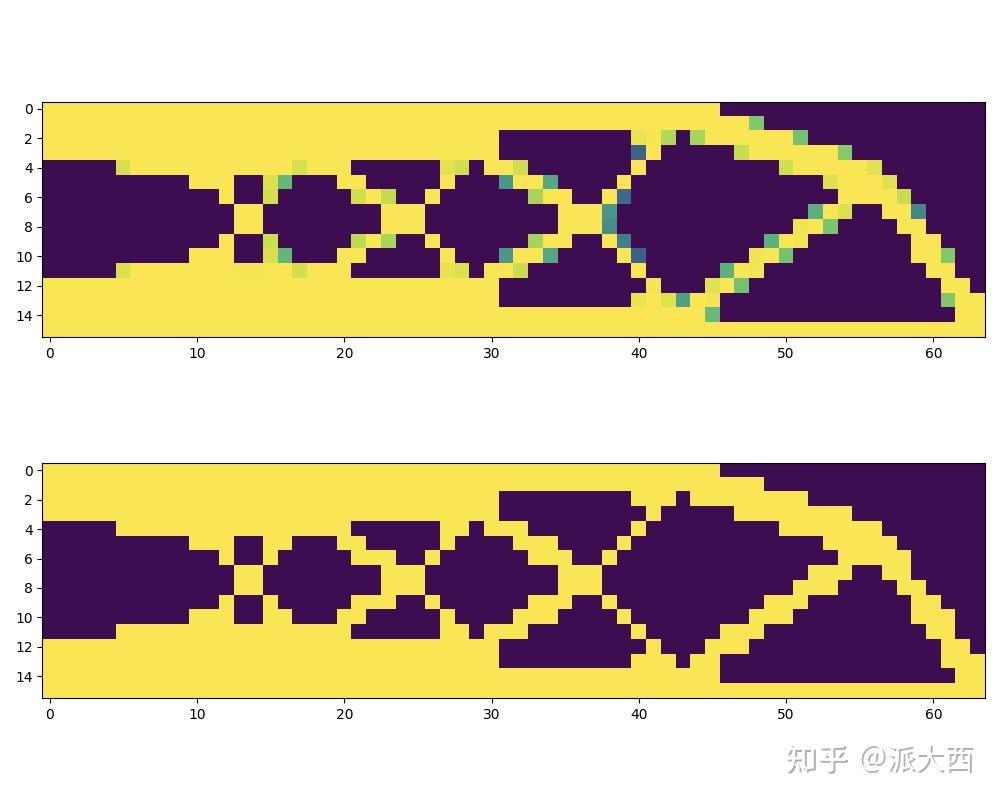
然后分别挂上负载，跟派大西徒手捏的对比一下：

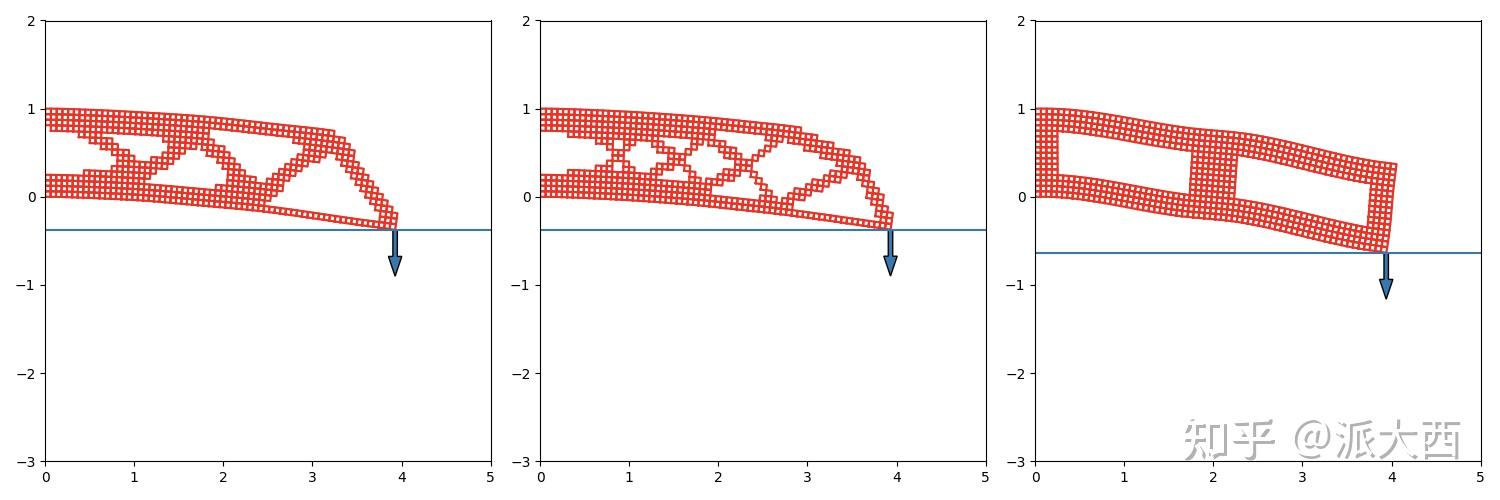
还是算出来的两位更厉害一点点，甚至还节省了不少材料。代码的话，还需要解有限元，这是前几节的老内容了：

def fea(nelx, nely, x, penal):
    K=np.zeros((2 * (nelx + 1) * (nely + 1), 2 * (nelx + 1) * (nely + 1)))
    F=np.zeros(2 * (nelx + 1) * (nely + 1))
    U=np.zeros(2 * (nelx + 1) * (nely + 1))
    for ely in range(nely):
        for elx in range(nelx):
            n1=(nely + 1) * elx + ely
            n2=(nely + 1) * (elx + 1) + ely
            edof=[2 * n1, 2 * n1 + 1, 2 * n2, 2 * n2 + 1, 2 * n2 + 2, 2 * n2 + 3, 2 * n1 + 2, 2 * n1 + 3, ]
            K[np.ix_(edof, edof)]+=x[ely, elx]** penal * local_stiff
    F[(nely + 1) * nelx * 2 + 1]=-1
    fixeddofs=[i for i in range((nely + 1) * 2)]
    alldofs=[i for i in range((nelx + 1) * (nely + 1) * 2)]
    freedofs=list(set(alldofs) - set(fixeddofs))
    U[np.ix_(freedofs)]=np.linalg.solve(K[np.ix_(freedofs, freedofs)], F[np.ix_(freedofs)])
    return U

把上面三个函数跟下面的主函数过程合并起来：

import numpy as np
import matplotlib.pyplot as plt

E=1000.
nv=0.3

w=np.array([1 / 2, 1 / 8, -1 / 4, -1 / 8, -1 / 4, -1 / 8, 0, 1 / 8]) - \\
    np.array([-1 / 6, 1 / 8, -1 / 12, 3 / 8, 1 / 12, -1 / 8, 1 / 6, -3 / 8]) * nv
local_stiff=E / (1 - nv ** 2) * np.stack([w,
                                            w[np.ix_([1, 0, 7, 6, 5, 4, 3, 2])],
                                            w[np.ix_([2, 7, 0, 5, 6, 3, 4, 1])],
                                            w[np.ix_([3, 6, 5, 0, 7, 2, 1, 4])],
                                            w[np.ix_([4, 5, 6, 7, 0, 1, 2, 3])],
                                            w[np.ix_([5, 4, 3, 2, 1, 0, 7, 6])],
                                            w[np.ix_([6, 3, 4, 1, 2, 7, 0, 5])],
                                            w[np.ix_([7, 2, 1, 4, 3, 6, 5, 0])]])

def top(nelx, nely, volfrac, penal, rmin):
    x=np.ones((nely, nelx)) * volfrac
    dc=np.zeros_like(x)
    loop=0
    change=1.
    while change > 0.0001 and loop < 1000:
        loop +=1
        xold=x.copy()
        U=fea(nelx, nely, x, penal)
        c=0.
        for ely in range(nely):
            for elx in range(nelx):
                n1=(nely + 1) * elx + ely
                n2=(nely + 1) * (elx + 1) + ely
                Ue=U[np.ix_([2 * n1, 2 * n1 + 1, 2 * n2, 2 * n2 + 1,
                               2 * n2 + 2, 2 * n2 + 3, 2 * n1 + 2, 2 * n1 + 3, ])]
                c +=x[ely, elx]** penal * np.sum(Ue * np.dot(local_stiff, Ue))
                dc[ely, elx]=-penal * x[ely, elx]** (penal - 1) * np.sum(Ue * np.dot(local_stiff, Ue))
        dc=smooth(nelx, nely, rmin, x, dc)
        x=OC(nelx, nely, x, volfrac, dc)
        change=np.abs(x - xold).max()
        print(f'Iteration{loop}:   Obj:{c:.4f}Vol:{x.sum() / nelx / nely:.4f}change:{change:.4f}')
    plt.imshow(x[::-1, :], vmin=0, vmax=1)
    return x

x=top(64, 16, 0.5, 3.0, 1.2)

虽然派大西写的代码跑得很慢，毕竟是个没怎么优化过的算法和代码。。能够伪实时计算的软件可以参考这里：

Interactive 2D TopOpt App - TopOpt

使用截图：

今天算是了解了一点拓扑优化，那么就到这儿吧～ @派大西

作者 | 王山 仿真秀科普作者

导读：轻量化是当今各整车厂在产品开发中无法回避的问题。当考虑到成本与工艺方面时，更是不容易解决的问题。对于高端车型，其较高的设计与生产成本允许其采用先进的轻量化设计与生产工艺，如碳纤维复合材料，铝镁合金材料，液压成型工艺，差厚板，激光拼焊等；对于低端车型来说，因较低的成本限制，则主要从结构设计角度来解决轻量化问题。但不论从材料，工艺还是结构方面实现轻量化，都需要借助CAE分析来提前预知结构性能。

白车身作为汽车主要承载部件，其质量占整车重量较大，通过合理设计，可减轻较多的质量，获得较为显著的轻量化效果。因而，车身的轻量化是开发阶段不可缺少且重点关注的部分。

这里所介绍的一种轻量化分析思路，是从结构设计与优化的角度，借助CAE仿真技术，来实现早期开发阶段的白车身结构从无到有，再到优的过程，起到控制车身性能和质量的目的，降低后期详细设计阶段车身性能与质量不可控的风险。

一、开发早期阶段的轻量化思路

在车身早期开发阶段中，一般情况下是没有车身的具体CAD数据。此时，为实现车身结构从无到有的过程，通过造型外CAS面及布置要求，制定车身拓扑空间，获得在考虑模态，刚度及碰撞等多个载荷工况下的车身载荷传递路径。结合此路径，来形成初版的车身结构形式布置方案。利用SFE-Concept隐式参数化建模技术实现布置方案的数字化与参数化，并得到初版的车身性能。（公开课-车身参数化建模及多目标优化技术，详见后文）

为实现从有到优的过程，通过对竞品车型结构研究及项目经验，同时必须结合初始性能分析结果，对于结果中较为薄弱的区域，选出具有代表性的结构形式，结合隐式参数化模型快速更替与修改能力，进行结构拓扑方案替换与性能验证，确保车身质量在基本保持不变的前提下，对车型性能进行提升，在项目计划时间内使车身结构性能尽可能最大化，目的是获取较大的减重空间。

之后利用断面尺寸优化与零件厚度优化，对车身进行减重分析，实现重量下降。由于该阶段并无具体性能目标，其减重优化工作应以减重前的性能水平为约束进行优化。待后续阶段制定具体目标值后可利用此模型再次进行减重优化分析，获得满足目标要求的轻量化车身结构。

二、某SUV车型白车身的轻量化分析案例

1、载荷传递路径分析

可利用Optistruct，Genesis等有限元软件的拓扑优化技术，以造型与内饰CAS面，动力总成占用空间，轮胎包络，车门门口，假人脚的位置，最小离地间隙，座椅安装位置，备胎占用空间等信息为输入条件，建立白车身拓扑优化空间，如图1所示。

图1 拓扑优化空间定义

车身的载荷传递路径获取需充分考虑车身各项整体性能要求，一般情况下，主要考虑NVH，刚度及碰撞三个学科，将白车身模态，弯扭刚度，正碰，侧碰，偏置碰，后碰及顶压作为考察工况。

经迭代计算后，可以获得多工况下的白车身载荷传递路径，如图2所示。

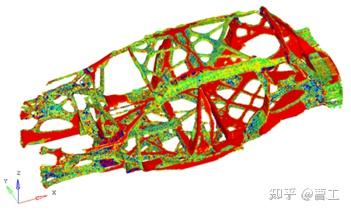
图2 白车身拓扑优化结果

拓扑优化分析结果需要进行解读，因为其结果为数值计算结果，并非考虑实际生产因素等方面的限制，所以需要筛选出主要的传递路径，此时应结合工程经验进行结构布置。识别出的各区域主要传递路径如图3所示，结构设计时可参考该路径对白车身纵梁及横梁进行布置。

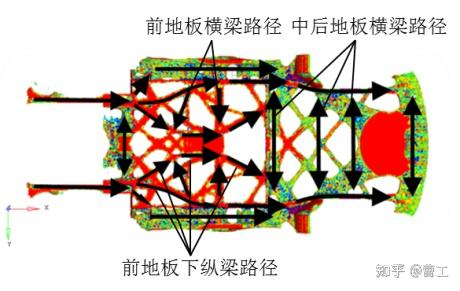
下车身主要传递路径

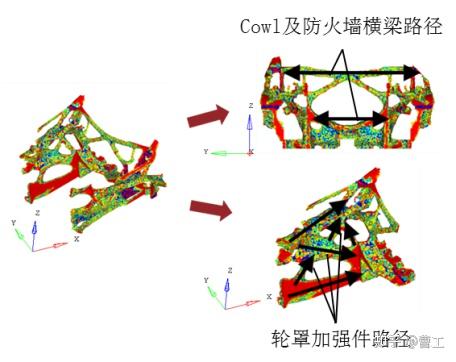
发舱主要传递路径

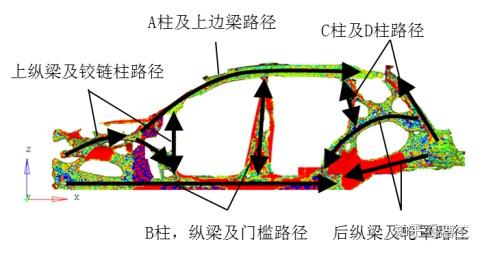
侧围主要传递路径

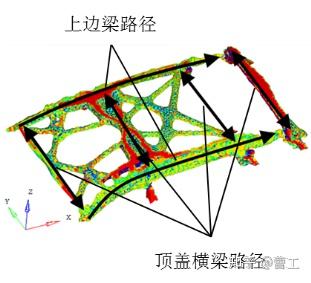
顶盖主要传递路径

图3 白车身各区域主要传递路径

2、隐式参数化模型建立与初始性能评估

在白车身布置方案确定后，在无需白车身CAD数据的情况下，仅以底盘硬点，典型断面，接头草数据，各零部件之间的搭建关系为输入条件，利用SFE-Concept软件便建立白车身隐式参数化模型，将从拓扑分析结果解读出来的设计概念变成清晰的三维数模，如图4所示。

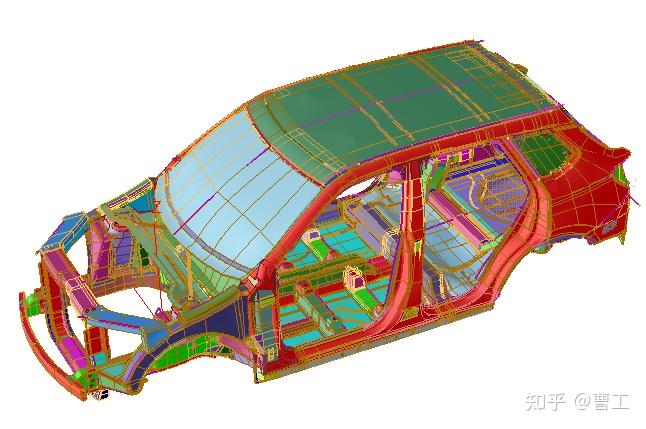
图4 白车身隐式参数化模型

隐式参数化建模技术是近些年来多数整车厂所采用的优化与轻量化分析工具，该建模技术能够在保证各部件连接完整性的前提下，实现结构的快速变形，如梁的位置移动，梁的截面尺寸修改等，因而可以融入到优化流程中，并且，可以一键快速生成满足后续有限元分析要求的网格。该技术的引用，使得以前使用morph功能对网格进行变形变得更加便捷。甚至，该参数化模型在车身开发中可替代第一版CAD模型。

本案例以白车身模态与弯扭刚度性能为主要考察指标，得到初始车身性能，如表2所示。从结果中可以看出，在考虑载荷传递路径分析结果下的白车身结构形式，其各项性能较好。

表1 白车身初始性能

汽车轻量化 | 某SUV车型白车身的轻量化分析案例（附公开课）

相关阅读推荐：

汽车减重之轻量化设计与仿真：整车开发过程中轻量化仿真分析流程与关键技术

1、附赠仿真学习包，包含结构、流体、电磁、热仿真等多学科教程，点击免费领取：知乎粉丝仿真学习包

2、免费阅读更多仿真干货文章：仿真图文教程

小白初学，做个笔记防止忘记。

拓扑优化技术可以针对零件的受力分析情况，去除掉零件不必要的结构，以达到减重和轻量化的目标，降低加工成本。

本人使用的版本为ansys 2021；

首先新建一个static structural和structural optimization，并将两个模块关联起来，鼠标左键按住拖动即可。

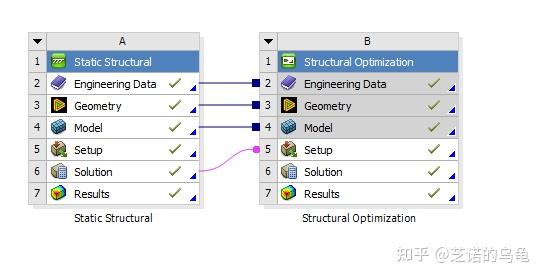
先点击A2的engineering data 编辑材料，然后进入材料库->explicit materials -> 点击钼（molybdenum）旁边的+号将其加入案例中，步骤如图2所示。

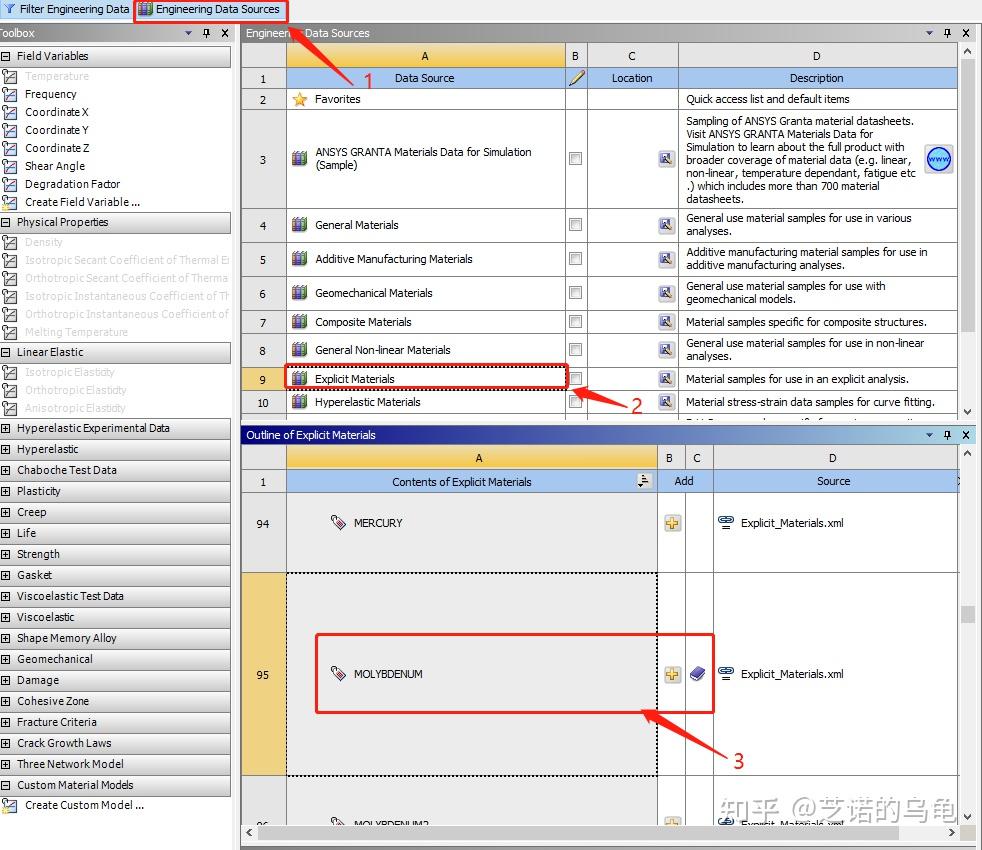
由于进行静力学分析和拓扑优化还需要设置材料的杨氏模量和泊松比等参数，单击钼材料->将isotropic elasticity拖入步骤3区域，然后输入钼的杨氏模量为329 GPa和泊松比为0.324；步骤如图3所示，接着关掉当前界面准备下一步建模。

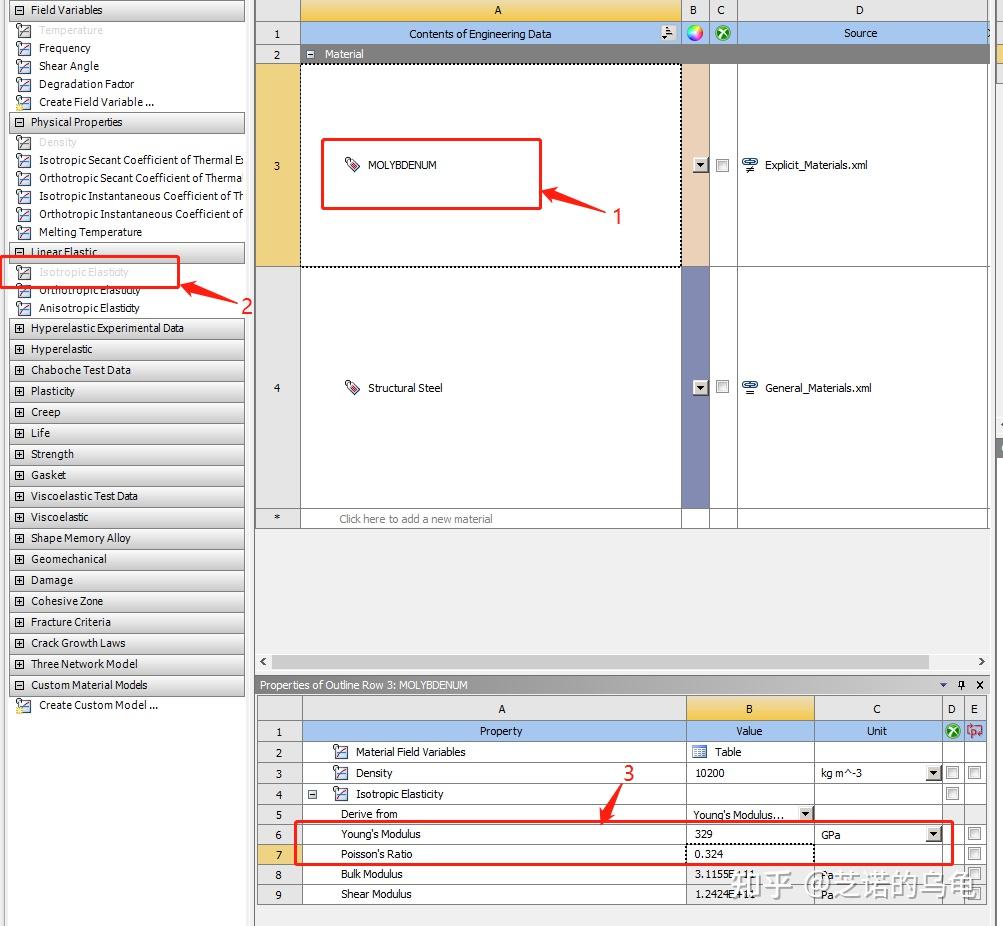
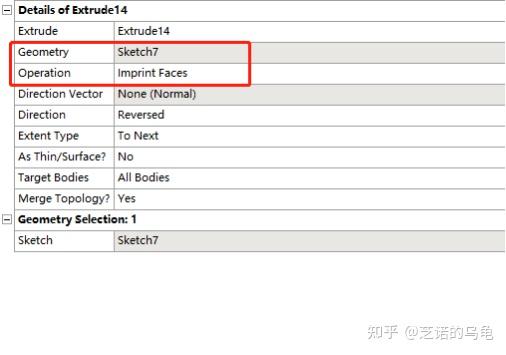
右键A3进入DesignModeler，模型如图4所示，为了方便后续施加螺栓的预紧力，这里需要在螺栓孔上新建印迹面（imprint face）。点击create -> new plane -> type选择 from face -> 鼠标点击固定架表面。然后切换到sketching 中绘制图5所示的四个同心圆环。

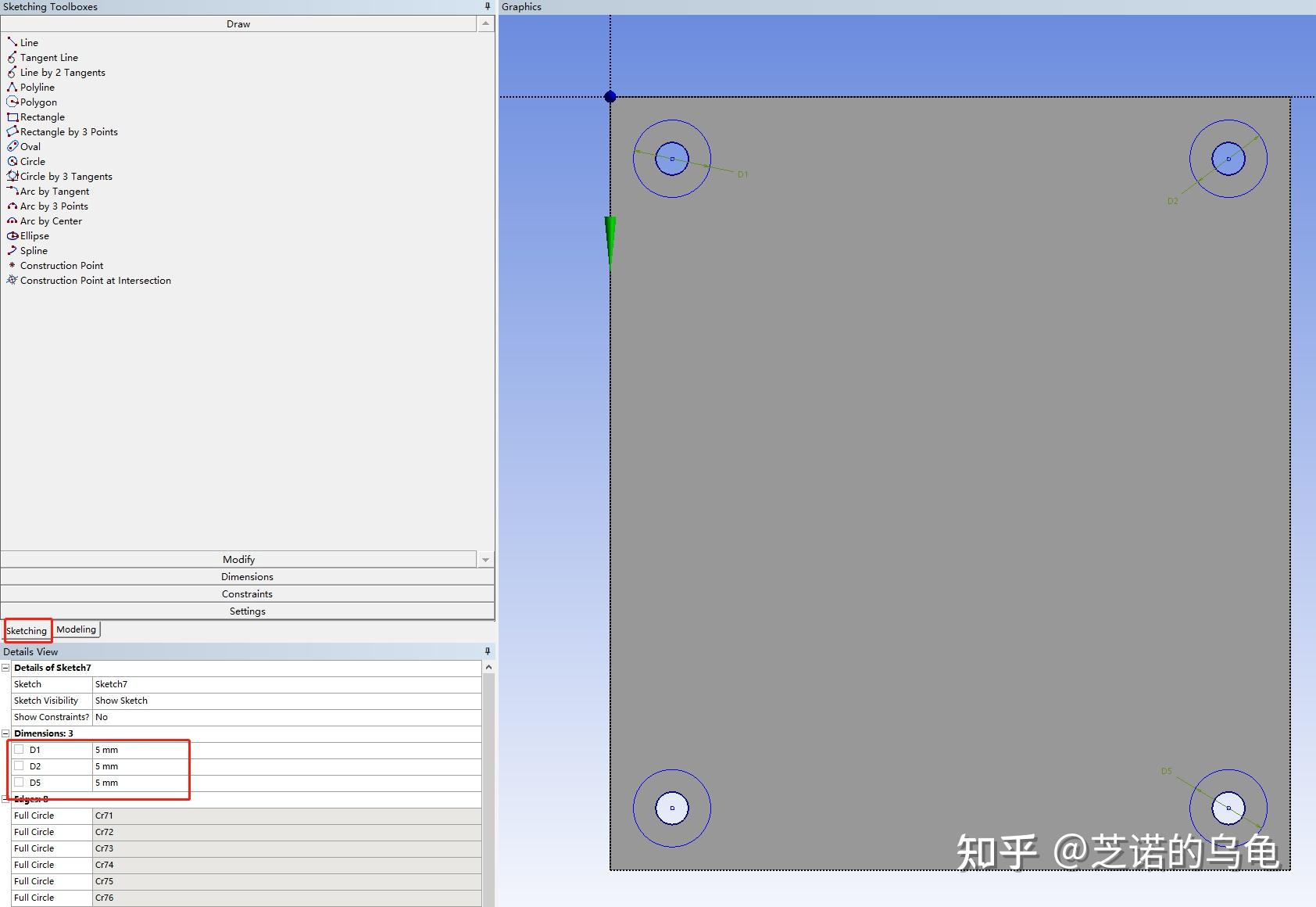
草图绘制完成后，点击generate，然后选择extrude -> geometry点选刚刚的草图 -> operation选择imprint faces，其余默认即可，点击generate。如图6所示。

先切换到面选择器，然后按住ctrl键选择刚刚完成的几个面，右键点击named selection，修改名称为face，作为后续的施力面，完成后点击generate。步骤如图7、8所示。

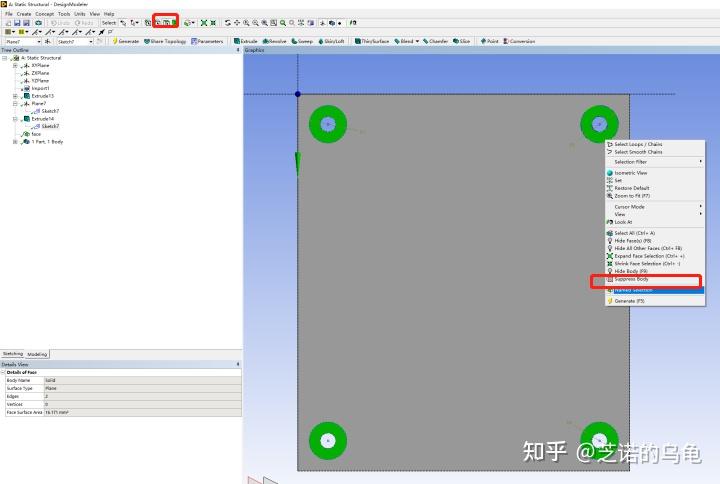
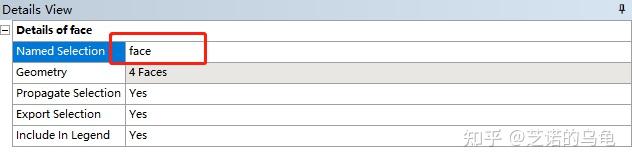
关掉design modeler，双击A5进入mechanical，进行网格划分和边界条件的设置；

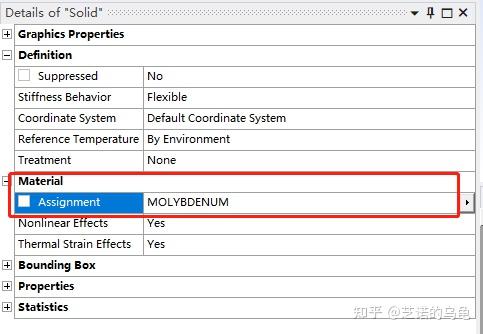
点击geometry下的solid，将其材料设置为钼，如图9所示；

右键mesh -> 插入face meshing -> 选中绘制的四个面 -> apply，如图10所示；

点击mesh -> element size 设置为1mm，也就是网格大小为1mm，如图11所示。

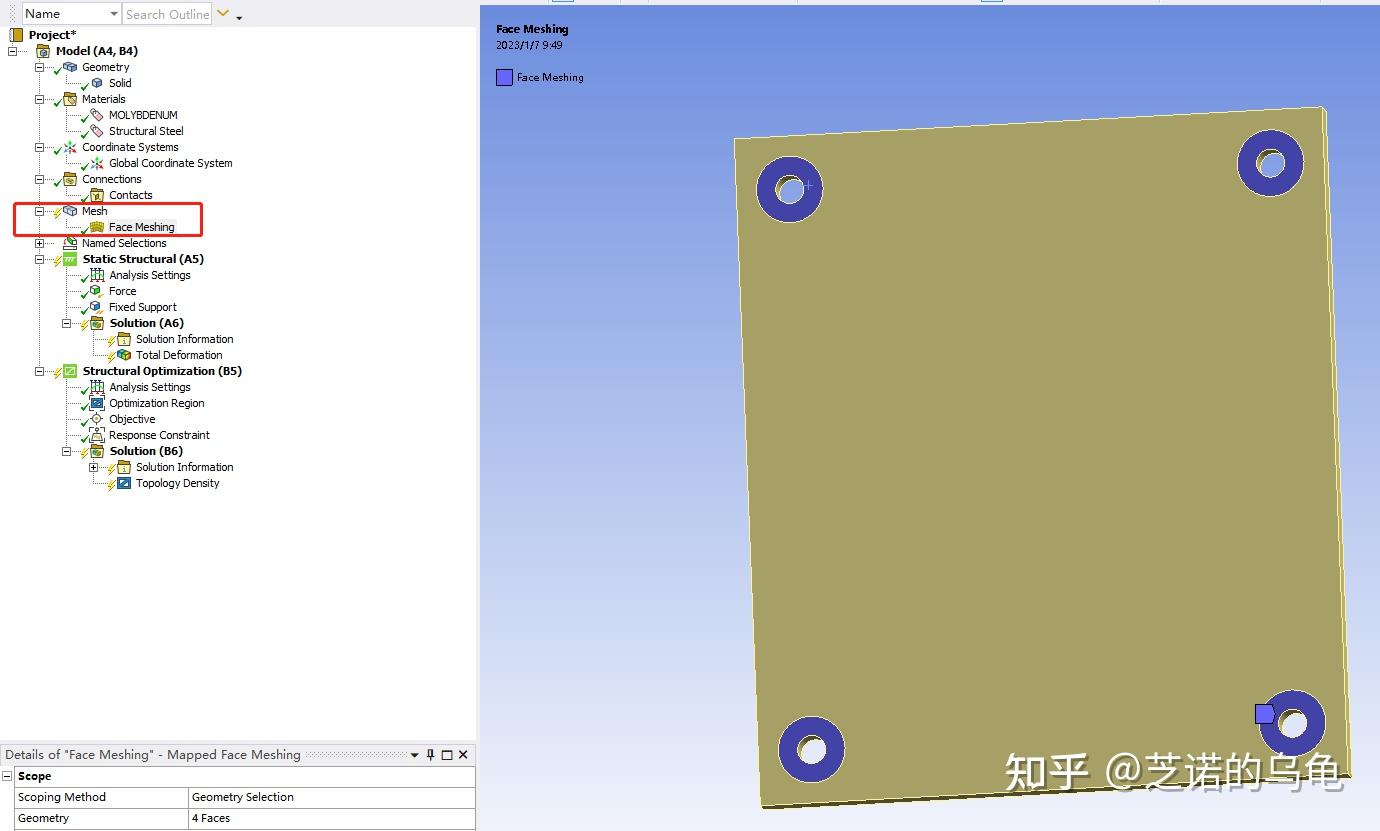
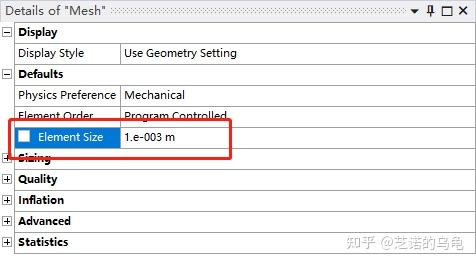
mesh 右键 generate mesh , 网格划分如图12所示，效果一般，但也勉强够用。

接着设置边界条件；

右键static structural（A5）-> insert -> force，大小设置为1 N，如图12所示；

然后右键static structural（A5）-> insert -> fixed support -> 选中背面 -> apply，如图13。

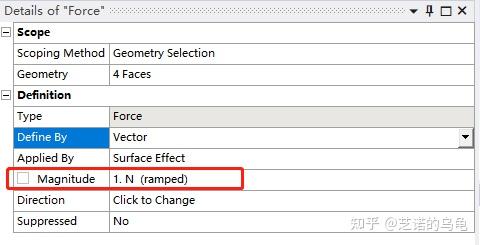
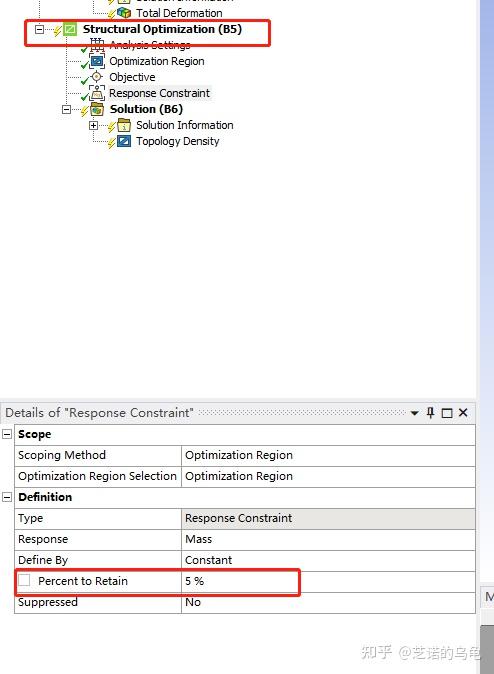
然后是拓扑优化条件的设置；

单击response constraint，将保留比例修改为5%（一般为30%，这里去除比较多，就改成了5%），如图14；

最后就点击solution，右键选择solve求解。

从图15、16、17中可以看到，当保留比例为30%时，部分地方仍存在一些多余的结构，轻量化效果不理想；保留比例为5%时，整个结构比较规整和光滑；保留比例到达1%时，有些地方则出现了空洞，这样的结果是不好的。

所以这里认为5%的保留比例是一个比较理想的结果，最后将其导出为STL文件，步骤如图18所示。

[1]钼的材料性能 http://rushmetal.com/Mo.html

[2]钼的主要物化性质 http://www.bjtrgs.com/html/2018/js2_1210/21.html

[3]DM中印迹面的添加 https://zhuanlan.zhihu.com/p/544394061

[4]桥梁拓扑优化简例 https://zhuanlan.zhihu.com/p/311207469

[5]fluent组分输运室内气体扩散计算 https://www.bilibili.com/video/BV1Yo4y1S7kC?vd_source=a3f75c4c4712e40ada955fc8a9aec7e1

想利用comsol对传热结构进行拓扑优化，拓扑优化之前需要先计算一下原来结构下温度场的情况，方便与拓扑优化以后的温度场进行对比。

但是在原温度场计算时，在材料设置选项中，我分别采用了两种方法：

方法1：直接插入材料对原结构材料进行设置，如下图所示

方法2：考虑到要对结构进行拓扑优化，在计算原结构温度场时便对材料进行了拓扑优化材料链接，如下图所示

然后分别对这两种方法下的原结构温度场进行了计算，计算结果发现两种方法的温度场存在较大的差别，其中方法2计算所得的温度场要高于方法1所得温度场。

有哪位大神知道这是为什么吗？为什么材料加了拓扑优化材料链接以后温度场会与不加拓扑优化材料链接的温度场不同吗？

拓扑优化由于具有极高的设计自由度，因此能实现极致的设计性能，但通过拓扑优化产生的设计往往无法通过传统的制造技术去实现生产。一直以来，研究用于拓扑优化的制造约束都是一个热点课题。COMSOL Multiphysics? 软件支持模拟铣削约束，在这篇文章中，我们将解释如何使用这种功能并介绍一些示例。

密度法是进行拓扑优化的最常见方法，在 COMSOL Multiphysics 中可以通过密度模型特征实现。最常见的应用是在结构力学领域，通常需要正则化才能获得有意义的结果。密度模型特征支持使用基于偏微分方程（PDE）的滤波器，也就是使用亥姆霍兹滤波器进行正则化。下图显示的结构力学示例显示了参数优化、形状优化和拓扑优化之间的差异。有关更多详细信息，请参阅文章“通过密度方法进行拓扑优化”。

图1 梁的设计优化模型示例，分别使用了参数优化、形状优化和拓扑优化解决结构力学中的问题。目标是在约束右上角位移下使梁质量最小。只有拓扑优化才能在设计中引入孔。

在密度模型 特征中，铣削约束是参考学术文献出版物（参考文献 1）来实现的。它的基本概念是使用一组在铣削方向 $\\hat{m}_\\mathrm{mil}^i$ 上具有对流的对流方程：

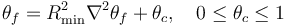
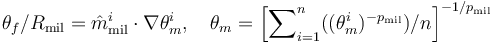
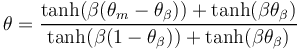
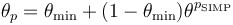
第一个方程是亥姆霍兹滤波器，使用控制变量场 $\ heta_c$ 来计算最小长度尺度为 $L_\\mathrm{min}$ 的过滤场 $\ heta_f$ 。对流方程（第二行）位于亥姆霍兹滤波器和投影之间。源项 $R_\\mathrm{mil}$ 的长度尺度通常可以根据网格大小设置。数值参数 $p_\\mathrm{mil}$ 与铣削变量 $\ heta_m^i$ 的聚合（指数）相关。对于 2~3 个铣削方向，数值 10 是合适的，但对于大量铣削方向可能需要高的值。投影斜率 $\\beta$ 也是如此，它比平时起着更重要的作用，因为投影的输入（第三行）通常明显大于 1。投影点 $\ heta_\\beta$ 固定为 0.5。使用投影场 $\ heta$ 对密度进行插值，对固体各向同性材料使用罚函数（SIMP）对刚度进行插值（最后一行， $\ heta_p$ ）。通常，使用 $p_\\mathrm{SIMP}$ =3 避免最终设计中的灰度，当数值问题导致投影场略为负值时，使用 $\ heta_\\mathrm{min}=10^{-3}$ 来确保鲁棒性。

我们只考虑单一材料的优化，因此体积 V 等同于质量 M，可以通过积分投影场并与密度 $\\rho$ 相乘来计算：

$M=\\rho V=\\rho\\int_\\Omega \ heta d\\Omega\\\\$

在公式中引入铣削约束会引入更多的局部最小值，并且在一系列优化被求解的情况下使用连续性可能是有益的。这大多数情况下是一个三维问题，所以与我们文中展示的第一个示例无关。

下图是对示例 1 的问题描述，与上一节中的问题一样，它也是一个结构力学问题，目标是约束右上角位移时使质量最小。但是这一次，由于施加了铣削约束，材料无法自由分布。此示例有两个与坐标轴重合的铣削方向，这意味着材料只能通过来自左侧或下方的“去除工具”去除。

图2.带铣削约束的梁拓扑优化模型的问题表述，包括铣削方向 $\\hat{m}_1$ 和 $\\hat{m}_2$ ，梁的左端是固定的，顶部边界则承受分布载荷。

带铣削约束的梁拓扑优化

如下图所示，密度模型特征具有铣削约束的设置。启用投影非常重要，而且很多时候还需要将控制变量场初始化为明显小于 1 的值。

图3. 启用铣削约束的示例，显示了密度模型特征的用户界面（UI）。投影部分在图中处于折叠状态，但在本例中，投影是使用默认斜率和投影点启用的。

在优化研究步骤中，定义了优化问题。MMA 是推荐的优化求解器方法，有时不使用全局收敛和/或移动限制是有益的。虽然使用默认的全耦合求解器也可以很好地实现优化求解，但上一节中的方程组包含一个用于过滤的线性方程，并使用两个用于对流的线性方程组形成单向耦合。最后一个方程与固体力学接口相关的方程组，还有另一种单向耦合。因此，使用分离式求解器求解要快得多。在这个示例中，分离式求解器将计算速度提高了约 2 倍。

图4.线性单向耦合问题的分离式求解器设置。使用固体力学接口定义线性系统时，甚至可以将求解器限制为单次迭代，来节省一点计算时间。或者，可以在固体力学接口步骤中使用多次迭代。

优化结果如下面的动画所示。在二维建模中，引入铣削约束可以防止产生孔，因此从这个意义上说，拓扑实际上是合适的，并且本质上该方法被简化为一种允许大变形的形状优化。因此，最适合使用铣削约束的是三维建模，我们将在接下来的两个示例中进行介绍。

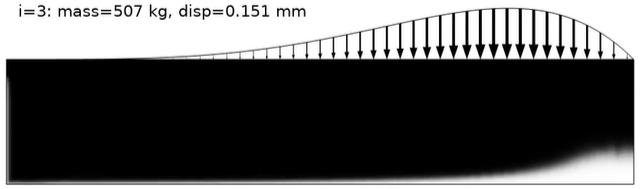
图示为不同的迭代次数绘制的材料体积因子 $\ heta$ 。无铣削约束的拓扑优化结果见图 1。

铣削约束降低了设计自由度，这应该更容易找到一个好的最优方案，但是由于还引入了非线性，在实践中，很容易得到局部最小值。如果分别在投影斜率 SIMP 指数 $\\beta$ 和 $p_\\mathrm{SIMP}$ 中使用连续策略，就可以在某种程度上避免这种情况。这种策略通常会产生良好的 3D 设计，但参数的选择可能对问题和铣削约束的数量很敏感。

考虑一个扭转球示例，这是一个经典的具有扭转荷载工况的基准问题，如下图所示。目标是最大限度地提高固定箱体和承受扭矩的箱体之间的刚度。这两个箱体沿扭矩轴分离，设计受到质量约束（相当于体积约束）。

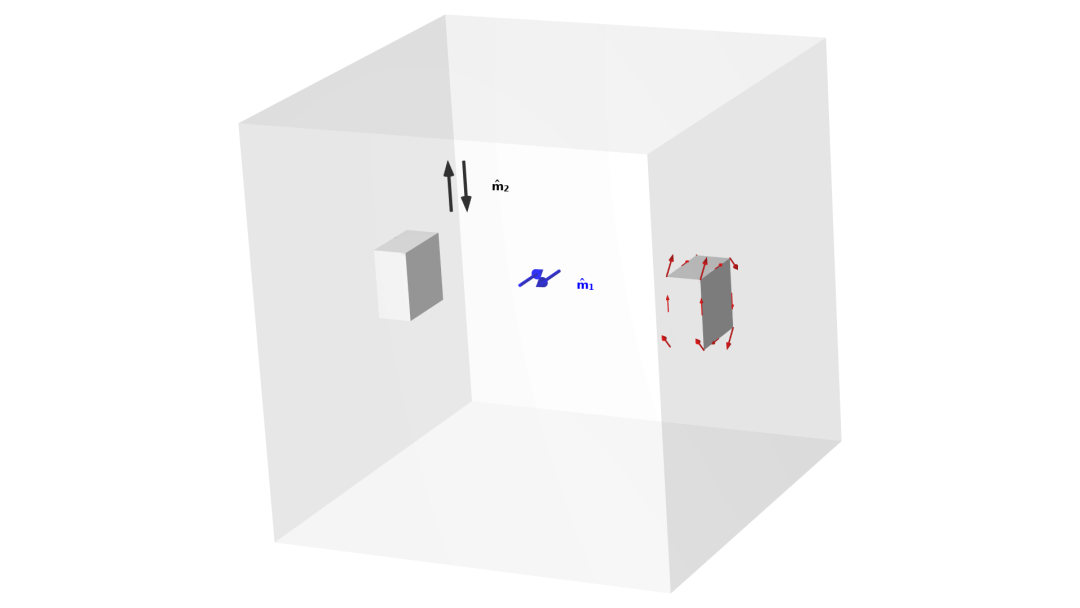
图5. 扭转球问题的设置。有 4 个铣削方向，但强加了对称性，因此只需要考虑 2 个铣削方向。

下面的动画显示，在带和不带铣削约束的情况下的优化结果。密度模型特征支持对流方程的线性离散化和常数离散化，这个示例演示了输出不太平滑的常数选项。

用灰度图绘制了带（右）和不带（左）铣削约束优化时 $0.5<\ heta$ 的单元。每次迭代都会显示目标值和连续参数。

对不带铣削约束的优化结果是一个含内腔的封闭球形设计。这种设计不可能用传统的减材制造方法制造，但非常适合测试制造约束。对带铣削约束进行优化会产生一个不含内腔的设计，但这是以柔度（刚度的倒数）高出约 40% 为代价的。如果不添加更多铣削方向，很难显著改进优化目标，但是拓扑对连续的细节还是很敏感的。

最后一个例子是一个三维结构问题。目标仍然是使受体积约束的刚度最大，但这个示例与前面的问题有三方面不同：

使用 12 个载荷工况而不是 1 个
扇区对称仅适用于设计（而不是物理场）
对流方程使用了线性离散化

使用 12 个载荷工况会导致更多的计算工作。但是，这些载荷工况可以并行计算，因此，如果有合适的硬件，计算时间不一定会大幅增加。

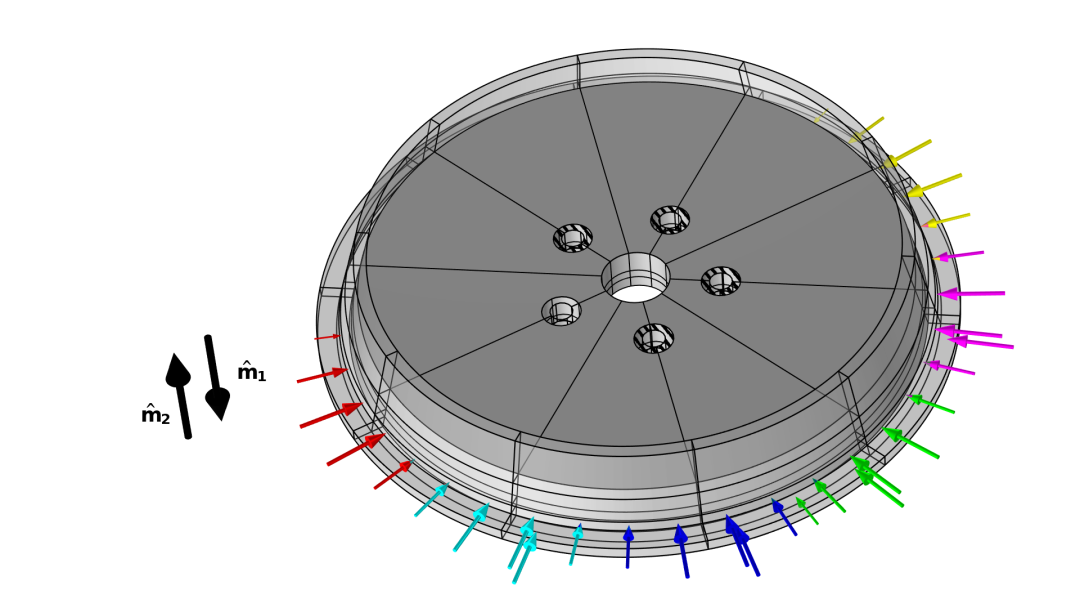
图6. 用各种颜色显示的载荷工况和用黑色显示的铣削方向来说明轮辋问题的设置。请注意，在轴向方向上还有第二组设置，并且只有四个螺栓孔受约束。

扇形区对称性是使用广义拉伸算子强加的，该算子将设计变量从“控制扇形区”映射到其他扇形区。

每次迭代都会显示目标值和连续参数。用灰度图绘制了带（右）和不带（左）铣削约束轮辋优化时） $0.5<\ heta$ 的单元。

在这个示例中，使用铣削约束进行优化生成的是含非分支辐条的简单拓扑。辐条的横截面具有 z 形形状，以增加两个方向的弯曲刚度。

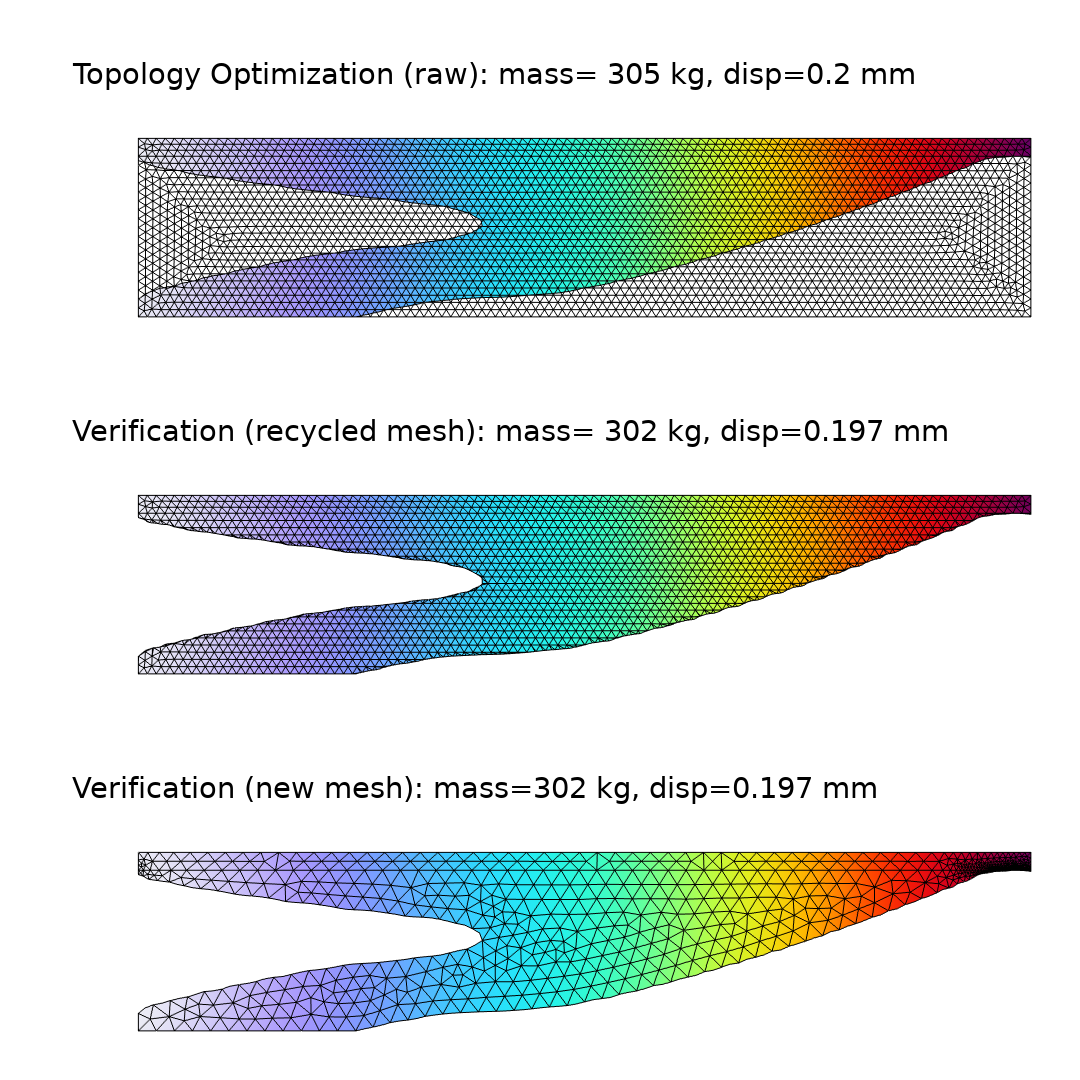
与密度方法相关的隐式几何表示总是会引入一些误差。这是由于非零刚度，以及实体和空隙之间过渡区域中的单元与较差的刚度质量比有关。后者的影响通常占主导地位，因此隐式几何表示法常常低估了性能。为了验证设计的性能，可以使用过滤器数据集将设计转移到一个新组件上。我们可以使用布尔表达式剪切单元，这样大部分网格就可以被回收，也可以将设计作为一个新的几何体导入并从头开始创建新网格，如下图所示。物理场接口（和特征）支持复制粘贴功能，因此简化了新组件的设置。物理场接口的选择将被重置，但在几何和定义下定义的所有选择都将自动转移到新的组件中使用。

图7.绘制了第一个示例（上图）的原始拓扑优化的位移场和网格。显示了带（中心）和不带（底部）回收网格的方法。在所有情况下，都绘制了示例的质量和约束。

如果您想要了解与进行拓扑优化有关的特征和功能的更多信息，请查看优化模块的介绍，单击下面的按钮，了解更多内容。

了解优化模块

L.C. H?gh?j and E.A. Tr?ff, “An advection-diffusion based filter for machinable designs in topology optimization,” Computer Methods in Applied Mechanics and Engineering, vol. 391, p. 114488, 2022; https://www.sciencedirect.com/science/article/pii/S0045782521007003

使用铣削约束进行拓扑优化

快捷链接

联系我们

扫描二维码